题目内容
三角形纸片ABC(AB>AC)沿过点A的直线折叠,使得AC落在AB边上,折痕为AD,展平纸片,如图;再次折叠该三角形纸片,使得点A与点D重合,折痕为EF,再次展平后连接DE、DF,如图,证明:四边形AEDF是菱形.

由第一次折叠可知:AD为∠CAB的平分线,∴∠1=∠2(2分)
由第二次折叠可知:∠CAB=∠EDF,∠1=∠3,∠2=∠4,
∵∠1=∠2,∴∠3=∠4(4分)
 ∵AD是△AED和△AFD的公共边,∴△AED≌△AFD(ASA)(6分)
∵AD是△AED和△AFD的公共边,∴△AED≌△AFD(ASA)(6分)
∴AE=AF,DE=DF
又由第二次折叠可知:AE=ED,AF=DF
∴AE=ED=DF=AF(8分)
故四边形AEDF是菱形.(9分)
解析:略

练习册系列答案
相关题目
 17、如图,钝角三角形纸片ABC中,∠BAC=110°,D为AC边的中点.现将纸片沿过点D的直线折叠,折痕与BC交于点E,点C的落点记为F.若点F恰好在BA的延长线上,则∠ADF=
17、如图,钝角三角形纸片ABC中,∠BAC=110°,D为AC边的中点.现将纸片沿过点D的直线折叠,折痕与BC交于点E,点C的落点记为F.若点F恰好在BA的延长线上,则∠ADF=

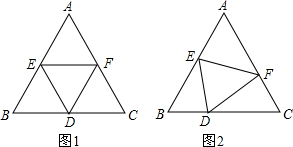
 如图,小明将三角形纸片ABC(AB>AC)沿过点A的直线折叠,使得AC落在AB边上,折痕为AD,展开纸片(如图①),再次折叠该三角形纸片,使点A和点D重合,折痕为EF,展平纸片后得到△AEF(如图②).小明认为△AEF是等腰三角形,你同意吗?请说明理由.
如图,小明将三角形纸片ABC(AB>AC)沿过点A的直线折叠,使得AC落在AB边上,折痕为AD,展开纸片(如图①),再次折叠该三角形纸片,使点A和点D重合,折痕为EF,展平纸片后得到△AEF(如图②).小明认为△AEF是等腰三角形,你同意吗?请说明理由.