题目内容
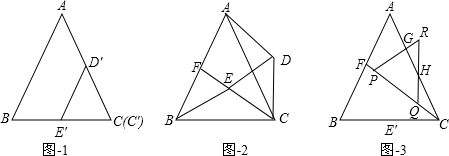
将等边三角形纸片ABC折叠,使点A落在对边BC上的点D处,折痕交AB于点E,交AC于点F.
(1)如图1,当BD=CD时,求证:AE=AF;
(2)如图2,当
=
时,求
的值;
(3)若
=
,请直接写出
的值(不需要过程).
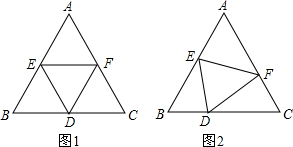
(1)如图1,当BD=CD时,求证:AE=AF;
(2)如图2,当
| BD |
| CD |
| 1 |
| 2 |
| AE |
| AF |
(3)若
| BD |
| CD |
| m |
| n |
| AE |
| AF |

分析:(1)连接AD,根据”三线合一“就得出∠DAE=∠DAF=30°,由轴对称可以得出AE=ED,AF=DF,进而可以得出△AED≌△AFD即可;
(2)由条件可以得出△BDE∽△CFD,设BD=x,CD=2x,就有BC=AB=AC=3x,设AE=DE=k,BE=3x-k,根据相似三角形的性质就可以表示出C、DF,再根据CF+DF=3x就可以求出x与k的数量关系,从而求出结论;
(3)由条件可以得出△BDE∽△CFD,设BD=mx,CD=nx,就有BC=AB=AC=mx+nx,设AE=DE=k,BE=mx+nx-k,根据相似三角形的性质就可以表示出C、DF,再根据CF+DF=mx+nx就可以求出x与k的数量关系,从而求出结论;
(2)由条件可以得出△BDE∽△CFD,设BD=x,CD=2x,就有BC=AB=AC=3x,设AE=DE=k,BE=3x-k,根据相似三角形的性质就可以表示出C、DF,再根据CF+DF=3x就可以求出x与k的数量关系,从而求出结论;
(3)由条件可以得出△BDE∽△CFD,设BD=mx,CD=nx,就有BC=AB=AC=mx+nx,设AE=DE=k,BE=mx+nx-k,根据相似三角形的性质就可以表示出C、DF,再根据CF+DF=mx+nx就可以求出x与k的数量关系,从而求出结论;
解答:解:(1)连接AD,
∵△ABC是等边三角形,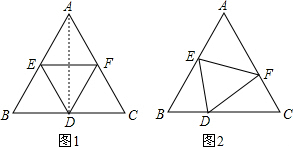
∴AB=BC=AC,∠A=∠B=∠C=60°.
∵BD=CD,
∴∠DAE=∠DAF=30°.
∵△AEF与△DEF关于EF对称,
∴AE=DE,AF=DF,
∴∠EDA=∠EAD=30°,∠FAD=∠FDA=30°,
∴∠EDA=∠EAD=∠FAD=∠FDA.
在△AED和△AFD中,
,
∴△AED≌△AFD(ASA),
∴AE=AF;
(2)∵△AEF与△DEF关于EF对称,
∴AE=DE,AF=DF,∠A=∠EDF=60°
∴∠BDE+∠CDF=120°.
∵∠BDE+∠BED=120°,
∴∠BED=∠CDF.
∵∠B=∠C,
∴△BDE∽△CFD,
∴
=
=
,
设BD=x,CD=2x,就有BC=AB=AC=3x,设AE=DE=k,BE=3x-k,
∴
=
,
∴CF=
.
∴
=
,
∴DF=
.
∵DF+CF=CF+AF=3x,
∴
+
=3x,
k=
x.
∴DF=
=
x,
∴
=
=
;
答:
的值为
;
(3))∵△AEF与△DEF关于EF对称,
∴AE=DE,AF=DF,∠A=∠EDF=60°
∴∠BDE+∠CDF=120°.
∵∠BDE+∠BED=120°,
∴∠BED=∠CDF.
∵∠B=∠C,
∴△BDE∽△CFD,
∴
=
=
,
设BD=mx,CD=nx,就有BC=AB=AC=mx+nx,设AE=DE=k,BE=mx+nx-k,
∴
=
,
∴CF=
.
∵
=
,
∴DF=
.
∵CF+DF=CF+AF=mx+nx,
∴
+
=mx+nx,
∴k=
,
∴DF=
=
.
∴
=
=
=
.
答:
的值为
.
∵△ABC是等边三角形,

∴AB=BC=AC,∠A=∠B=∠C=60°.
∵BD=CD,
∴∠DAE=∠DAF=30°.
∵△AEF与△DEF关于EF对称,
∴AE=DE,AF=DF,
∴∠EDA=∠EAD=30°,∠FAD=∠FDA=30°,
∴∠EDA=∠EAD=∠FAD=∠FDA.
在△AED和△AFD中,
|
∴△AED≌△AFD(ASA),
∴AE=AF;
(2)∵△AEF与△DEF关于EF对称,
∴AE=DE,AF=DF,∠A=∠EDF=60°
∴∠BDE+∠CDF=120°.
∵∠BDE+∠BED=120°,
∴∠BED=∠CDF.
∵∠B=∠C,
∴△BDE∽△CFD,
∴
| BD |
| CF |
| BE |
| CD |
| DE |
| FD |
设BD=x,CD=2x,就有BC=AB=AC=3x,设AE=DE=k,BE=3x-k,
∴
| x |
| CF |
| 3x-k |
| 2x |
∴CF=
| 2x2 |
| 3x-k |
∴
| 3x-k |
| 2x |
| k |
| DF |
∴DF=
| 2xk |
| 3x-k |
∵DF+CF=CF+AF=3x,
∴
| 2x2 |
| 3x-k |
| 2xk |
| 3x-k |
k=
| 7 |
| 5 |
∴DF=
2x•
| ||
3x-
|
| 7 |
| 4 |
∴
| DE |
| DF |
| AE |
| AF |
| 4 |
| 5 |
答:
| AE |
| AF |
| 4 |
| 5 |
(3))∵△AEF与△DEF关于EF对称,
∴AE=DE,AF=DF,∠A=∠EDF=60°
∴∠BDE+∠CDF=120°.
∵∠BDE+∠BED=120°,
∴∠BED=∠CDF.
∵∠B=∠C,
∴△BDE∽△CFD,
∴
| BD |
| CF |
| BE |
| CD |
| DE |
| FD |
设BD=mx,CD=nx,就有BC=AB=AC=mx+nx,设AE=DE=k,BE=mx+nx-k,
∴
| mx |
| CF |
| mx+nx-k |
| nx |
∴CF=
| mnx2 |
| mx+nx-k |
∵
| mx+nx-k |
| nx |
| k |
| DF |
∴DF=
| knx |
| mx+nx-k |
∵CF+DF=CF+AF=mx+nx,
∴
| mnx2 |
| mx+nx-k |
| knx |
| mx+nx-k |
∴k=
| m2x+n2x+mnx |
| 2n+m |
∴DF=
| ||
mx+nx-
|
| (m2+n2+mn)x |
| 2m+n |
∴
| DE |
| DF |
| AE |
| AF |
| ||
|
| 2m+n |
| 2n+m |
答:
| AE |
| AF |
| 2m+n |
| 2n+m |
点评:本题考查了等边三角形的性质的运用,轴对称的性质的运用,全等三角形的判定与性质的运用,相似三角形的判定与性质的运用,解答时运用相似三角形的性质建立方程求解是关键.

练习册系列答案
 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案
相关题目
 ,求y与x之间的函数解析式,并写出函数自变量x的取值范围.
,求y与x之间的函数解析式,并写出函数自变量x的取值范围.