题目内容
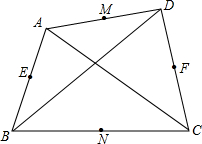 如图,在四边形ABCD中,AC、BD为对角线,点M、E、N、F分别为AD、AB、BC、CD边的中点,下列说法:
如图,在四边形ABCD中,AC、BD为对角线,点M、E、N、F分别为AD、AB、BC、CD边的中点,下列说法:①当AC=BD时,M、E、N、F四点共圆.
②当AC⊥BD时,M、E、N、F四点共圆.
③当AC=BD且AC⊥BD时,M、E、N、F四点共圆.
其中正确的是( )
| A、①② | B、①③ | C、②③ | D、①②③ |
考点:四点共圆,三角形中位线定理,菱形的判定与性质,矩形的判定与性质,正方形的判定与性质
专题:
分析:连接EM、MF、FN、NE,连接EF、MN,交于点O,利用三角形中位线定理可证到四边形ENFM是平行四边形;然后根据条件判定四边形ENFM的形状,就可知道M、E、N、F四点是否共圆.
解答: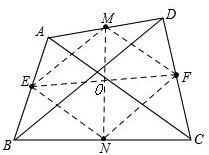 解:连接EM、MF、FN、NE,连接EF、MN,交于点O,如图所示.
解:连接EM、MF、FN、NE,连接EF、MN,交于点O,如图所示.
∵点M、E、N、F分别为AD、AB、BC、CD边的中点,
∴EM∥BD∥NF,EN∥AC∥MF,EM=NF=
BD,EN=MF=
AC.
∴四边形ENFM是平行四边形.
①当AC=BD时,
则有EM=EN,
所以平行四边形ENFM是菱形.
而菱形的四个顶点不一定共圆,
故①不一定正确.
②当AC⊥BD时,
由EM∥BD,EN∥AC可得:EM⊥EN,即∠MEN=90°.
所以平行四边形ENFM是矩形.
则有OE=ON=OF=OM.
所以M、E、N、F四点共圆,
故②正确.
③当AC=BD且AC⊥BD时,
同理可得:四边形ENFM是正方形.
则有OE=ON=OF=OM.
所以M、E、N、F四点共圆,
故③正确.
故选:C.
 解:连接EM、MF、FN、NE,连接EF、MN,交于点O,如图所示.
解:连接EM、MF、FN、NE,连接EF、MN,交于点O,如图所示.∵点M、E、N、F分别为AD、AB、BC、CD边的中点,
∴EM∥BD∥NF,EN∥AC∥MF,EM=NF=
| 1 |
| 2 |
| 1 |
| 2 |
∴四边形ENFM是平行四边形.
①当AC=BD时,
则有EM=EN,
所以平行四边形ENFM是菱形.
而菱形的四个顶点不一定共圆,
故①不一定正确.
②当AC⊥BD时,
由EM∥BD,EN∥AC可得:EM⊥EN,即∠MEN=90°.
所以平行四边形ENFM是矩形.
则有OE=ON=OF=OM.
所以M、E、N、F四点共圆,
故②正确.
③当AC=BD且AC⊥BD时,
同理可得:四边形ENFM是正方形.
则有OE=ON=OF=OM.
所以M、E、N、F四点共圆,
故③正确.
故选:C.
点评:本题考查了四点共圆、三角形的中位线定理、平行四边形的判定与性质、矩形的判定与性质、菱形的判定与性质、正方形的判定与性质等知识.在解决问题的过程中,可能会把AC、BD误认为是平行四边形ENFM的对角线,从而由AC=BD得到该四边形是矩形这样一个错误结论,需加以注意.

练习册系列答案
相关题目
在下面的汽车标志图形中,是中心对称图形但不是轴对称图形有( )
A、 |
B、 |
C、 |
D、 |
直线y=kx+b经过A(0.2)和B(3.0)两点,那么这个一次函数关系式是( )
| A、y=2x+3 | ||
B、y=-
| ||
| C、y=3x+2 | ||
| D、y=x+1 |
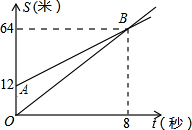 如图,OB、AB分别表示甲、乙两名同学运动的一次函数图象,图中s和t分别表示运动路程和时间.已知甲的速度比乙快,下列说法:①射线AB表示甲的路程与时间的函数关系;②甲的速度比乙快10.5m/s;③甲让乙先跑了12m;④8秒钟后,甲超过了乙,其中正确的说法是( )
如图,OB、AB分别表示甲、乙两名同学运动的一次函数图象,图中s和t分别表示运动路程和时间.已知甲的速度比乙快,下列说法:①射线AB表示甲的路程与时间的函数关系;②甲的速度比乙快10.5m/s;③甲让乙先跑了12m;④8秒钟后,甲超过了乙,其中正确的说法是( )| A、①② | B、②③④ |
| C、②③ | D、①③④图3 |
点P(m+1,n)向下平移4个单位后,关于y轴对称的点的坐标为(-1,-5),则点P的坐标为( )
| A、(1,-1) |
| B、(1,1) |
| C、(-1,1) |
| D、(-1,-1) |