题目内容
若关于x的一元二次方程(k-1)x2-2x+1=0有整数根,则负整数k的值为 .
考点:根的判别式
专题:计算题
分析:根据判别式的意义得到k-1≠0且△=(-2)2-4(k-1)=4(2-k)≥0,解得k≤2且k≠1,再利用求根公式得x=
,根据题意2-k为完全平方数,且x有整数,则2-k=4,即可得到k=-2.
1±
| ||
| k-1 |
解答:解:根据题意得k-1≠0且△=(-2)2-4(k-1)=4(2-k)≥0,
解得k≤2且k≠1,
x=
,
因为原方程有整数根,则2-k=4时,即k=-2时,x有整数.
故答案为-2.
解得k≤2且k≠1,
x=
1±
| ||
| k-1 |
因为原方程有整数根,则2-k=4时,即k=-2时,x有整数.
故答案为-2.
点评:本题考查了根的判别式:一元二次方程ax2+bx+c=0(a≠0)的根与△=b2-4ac有如下关系:当△>0时,方程有两个不相等的两个实数根;当△=0时,方程有两个相等的两个实数根;当△<0时,方程无实数根.

练习册系列答案
相关题目
 如图,AC⊥BC,AD⊥DB,还需要什么条件,就可以使△ABC≌△BAD,把所需要的条件写在横线上.
如图,AC⊥BC,AD⊥DB,还需要什么条件,就可以使△ABC≌△BAD,把所需要的条件写在横线上. 如图,已知△ABO的顶点A和AB边的中点C都在双曲线y=
如图,已知△ABO的顶点A和AB边的中点C都在双曲线y= 如图,在△ABC中,∠C=90°,AC=12cm,AB=25cm,点D在BC上,DE⊥AB,垂足为E,且DE=DC,则BE=
如图,在△ABC中,∠C=90°,AC=12cm,AB=25cm,点D在BC上,DE⊥AB,垂足为E,且DE=DC,则BE=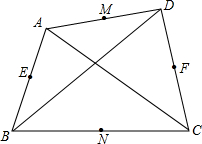 如图,在四边形ABCD中,AC、BD为对角线,点M、E、N、F分别为AD、AB、BC、CD边的中点,下列说法:
如图,在四边形ABCD中,AC、BD为对角线,点M、E、N、F分别为AD、AB、BC、CD边的中点,下列说法: