题目内容
如图，D、E、F内分正△ABC的三边AB、BC、AC均为1：2两部分，AD、BE、CF相交成的△PQR的面积是△ABC的面积的（ ）A、
| ||
B、
| ||
C、
| ||
D、
|
分析：根据梅涅劳斯定理得出
=
，再由三角形面积的求法得出S△PQR=S△BCF-S△BCQ-SBPRF=
S△ABC，从而得出答案．
| AP |
| PD |
| 6 |
| 1 |
| 1 |
| 7 |
解答：解：对△ADC用梅涅劳斯定理可以得：
•
•
=1，则
=
．
设S△BCF=
，S△BCQ=
S△BCE=
，SBPRF=
S△ABD=
，
∴S△PQR=S△BCF-S△BCQ-SBPRF=
S△ABC．
故选D．
| AP |
| PD |
| DB |
| BC |
| CE |
| EA |
| AP |
| PD |
| 6 |
| 1 |
设S△BCF=
| 2 |
| 3 |
| 6 |
| 7 |
| 6 |
| 21 |
| 5 |
| 7 |
| 5 |
| 21 |
∴S△PQR=S△BCF-S△BCQ-SBPRF=
| 1 |
| 7 |
故选D．
点评：本题考查了梅涅劳斯定理和赛瓦定理，要熟练掌握定理的内容是解题的关键．
练习册系列答案
相关题目
如图，是由四个直角边分别是6和8的全等的直角三角形拼成的“赵爽弦图”，如果某人随机地往大正方形区域内投针一次，则针扎在阴影部分的概率为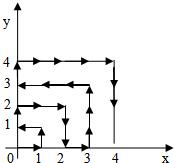
如图：一个粒子在第一象限内及x轴，y轴上运动，在第一分钟内，它从原点运动到（1，0），第二分钟从（1，0）运动到（1，1），而后它接着按图中箭头所示在与x轴，y轴平行的方向来回运动，且每分钟移动1个长度单位．
如图，点P为矩形ABCD内一点，作平行四边形ABQP，连接CP、CQ、BP，E、F、G、H分别是BP、BQ、CQ、CP的中点，