题目内容
 如图,点P为矩形ABCD内一点,作平行四边形ABQP,连接CP、CQ、BP,E、F、G、H分别是BP、BQ、CQ、CP的中点,
如图,点P为矩形ABCD内一点,作平行四边形ABQP,连接CP、CQ、BP,E、F、G、H分别是BP、BQ、CQ、CP的中点,(1)四边形EFGH的形状是
矩形
矩形
;(2)若矩形ABCD的面积为S,则四边形EFGH的面积等于
| 1 |
| 4 |
| 1 |
| 4 |
分析:(1)根据三角形的中位线定理可以证得:HG∥EF,且HG=EF,则四边形EFGH是平行四边形,然后根据平行线的性质可以证得∠HEF=90°,则平行四边形EFGH是矩形;
(2)首先根据题意可得S四边形PBQC=
S矩形ABCD=
S,再根据S矩形HGFE=
S四边形PBQC,可得答案.
(2)首先根据题意可得S四边形PBQC=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解答:证明:∵E,F分别是BP,BQ的中点,
∴EF∥PQ且EF=
PQ,
同理,GH∥PQ,GH=
PQ,EH∥BC,
∴HG∥EF,且HG=EF,
∴四边形EFGH是平行四边形.
∵PQ∥BA∥HG,
∴∠FMC=∠ABC=90°,
∵EH∥CB,
∴∠HEF=∠FMC=90°,
∴平行四边形EFGH是矩形;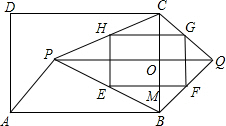
(2)S四边形PBQC=S△PBC+S△CBQ=
×BC×PO+
BC×QO=
BC•(PO+QO)=
CB•PQ,
∵四边形ABQP是平行四边形,
∴AB=QP,
∴S四边形PBQC=
BC•AB=
S矩形ABCD=
S,
∵E、F、G、H分别是BP、BQ、CQ、CP的中点,
∴S矩形HGFE=
S四边形PBQC=
S.
故答案为:
S.
∴EF∥PQ且EF=
| 1 |
| 2 |
同理,GH∥PQ,GH=
| 1 |
| 2 |
∴HG∥EF,且HG=EF,
∴四边形EFGH是平行四边形.
∵PQ∥BA∥HG,
∴∠FMC=∠ABC=90°,
∵EH∥CB,
∴∠HEF=∠FMC=90°,
∴平行四边形EFGH是矩形;

(2)S四边形PBQC=S△PBC+S△CBQ=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∵四边形ABQP是平行四边形,
∴AB=QP,
∴S四边形PBQC=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∵E、F、G、H分别是BP、BQ、CQ、CP的中点,
∴S矩形HGFE=
| 1 |
| 2 |
| 1 |
| 4 |
故答案为:
| 1 |
| 4 |
点评:此题主要考查了中点四边形,关键是掌握三角形中位线定理:三角形的中位线平行于三角形的第三边,并且等于第三边的一半.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 如图,点E为矩形ABCD的边AD上一点,BE=BC,EF平分∠AEB交AB于点F,连FC.
如图,点E为矩形ABCD的边AD上一点,BE=BC,EF平分∠AEB交AB于点F,连FC.
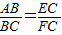 .
.