题目内容
若b（b≠0）是方程x2+cx+b=0的根，则b+c的值为
- A.1
- B.-1
- C.2
- D.-2
B
分析：一元二次方程的根就是一元二次方程的解，就是能够使方程左右两边相等的未知数的值．即用这个数代替未知数所得式子仍然成立．
解答：把x=b代入方程x2+cx+b=0得到：b2+bc+b=0即b（b+c+1）=0，又∵b≠0，∴b+c=-1，
故本题选B．
点评：本题考查的是一元二次方程的根即方程的解的定义．
分析：一元二次方程的根就是一元二次方程的解，就是能够使方程左右两边相等的未知数的值．即用这个数代替未知数所得式子仍然成立．
解答：把x=b代入方程x2+cx+b=0得到：b2+bc+b=0即b（b+c+1）=0，又∵b≠0，∴b+c=-1，
故本题选B．
点评：本题考查的是一元二次方程的根即方程的解的定义．
练习册系列答案
阅读快车系列答案
相关题目
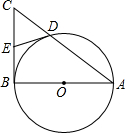在Rt△ABC中，直角边AB为直径的半圆O，与斜边AC交于D，点E是BC边的中点，连接DE，
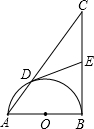如图，以Rt△ABC的直角边AB为直径的半圆O，与斜边AC交于D，E是BC边上的中点，连接DE．