题目内容
若m（m≠0）是方程x2+nx+m=0的根，则m+n的值是（ ）
分析：将m代入x2+nx+m=0，得m2+nm+m=0，再适当变形整理即可．
解答：解：把m代入x2+nx+m=0，得m2+nm+m=0，
∴m（m+n+1）=0，
又∵m≠0，∴m+n+1=0，
∴m+n=-1，
故选B．
∴m（m+n+1）=0，
又∵m≠0，∴m+n+1=0，
∴m+n=-1，
故选B．
点评：本题考查了一元二次方程的解，重点考查综合运用所给已知条件处理问题的能力．
练习册系列答案
阅读快车系列答案
相关题目
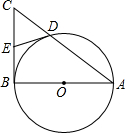在Rt△ABC中，直角边AB为直径的半圆O，与斜边AC交于D，点E是BC边的中点，连接DE，
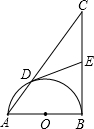如图，以Rt△ABC的直角边AB为直径的半圆O，与斜边AC交于D，E是BC边上的中点，连接DE．