题目内容
【题目】问题情境:如图,已知AB∥CD,∠1=∠2,求证:∠3=∠4.

解法展示:证明:延长BE交直线CD于点M,如图所示.

∵AB∥CD,∴∠1=∠BMC(根据1).
∵∠1=∠2,∴∠2=∠BMC(根据2).
∴BE∥CF(根据3).
∴∠3=∠4(根据4).
反思交流:(1)解法展示中的根据1是______________,根据2是______________,根据3是_____________,根据4是____________.
(2)上述命题中,条件记为:①AB∥CD,②∠1=∠2,结论记为:③∠3=∠4.若把其中的一个条件和结论对调,得到一个新命题,写出这个命题(用序号表示即可),判断新命题的真假,并说明理由.
【答案】(1)两直线平行,内错角相等 ; 等量代换 ; 同位角相等,两直线平行 ; 两直线平行,内错角相等;(2)已知:①③,求证:②;是真命题,见解析.
【解析】
延长BE交直线CD于点M,利用平行线的性质和判定定理进行证明即可.
解:(1)证明:延长BE交直线CD于点M,如图所示.
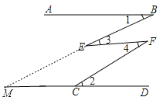
∵AB∥CD,∴∠1=∠BMC(两直线平行,内错角相等).
∵∠1=∠2,∴∠2=∠BMC(等量代换).
∴BE∥CF(同位角相等,两直线平行).
∴∠3=∠4(两直线平行,内错角相等).
故答案为:两直线平行,内错角相等;等量代换; 同位角相等,两直线平行; 两直线平行,内错角相等.
(2)交换①和③或交换②和③都是真命题.选择交换②和③,成为新命题.
已知:①③,求证:②.
理由:如图,延长BE交直线CD于点M.

∵∠3=∠4,
∴BE∥CF.
∴∠2=∠BMC.
∵AB∥CD,
∴∠1=∠BMC
.∴∠1=∠2.

【题目】2019年4月23日世界读书日这天,滨江初二年级的学生会,就2018年寒假读课外书数量(单位:本)做了调查,他们随机调查了甲、乙两个班的10名同学,调查过程如下
收集数据
甲、乙两班被调查者读课外书数量(单位:本)统计如下:
甲:1,9,7,4,2,3,3,2,7,2
乙:2,6,6,3,1,6,5,2,5,4
整理、描述数据绘制统计表如下,请补全下表:
班级 | 平均数 | 众数 | 中位数 | 方差 |
甲 | 4 | 3 | ||
乙 | 6 | 3.2 |
分析数据、推断结论
(1)该校初二乙班共有40名同学,你估计读6本书的同学大概有_____人;
(2)你认为哪个班同学寒假读书情况更好,写出理由.