题目内容
1. 如图,城市人行天桥的引桥由楼梯AD、EB和一段水平平台DE构成,AD与EB互相平行并且与地面成37°角.已知引桥的高BC=6m,引桥的水平跨度AC=12m.
如图,城市人行天桥的引桥由楼梯AD、EB和一段水平平台DE构成,AD与EB互相平行并且与地面成37°角.已知引桥的高BC=6m,引桥的水平跨度AC=12m.(1)求两段楼梯AD、EB的总长度;
(2)求水平平台DE的长.
【参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75】
分析 (1)首先延长BE交AC于点F,由AD∥BE,可得∠BFC=∠A=37°,又由桥的高BC=6m,可求得CF的长,继而求得BF的长,又由AD∥BE,DE∥AC,可得四边形ADEF是平行四边形,即可得AD+BE=BF=10m;
(2)由四边形ADEF是平行四边形,可得DE=AF=AC-CF.
解答 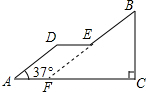 解:(1)延长BE交AC于点F,
解:(1)延长BE交AC于点F,
∵AD∥BE,
∴∠BFC=∠A=37°,
又∵BC⊥AC,即∠C=90°,
∴tan∠BFC=$\frac{BC}{FC}$,
∴FC=$\frac{BC}{tan∠BFC}$=$\frac{6}{tan37°}$≈$\frac{6}{0.75}$=8(m),
∴BF=$\sqrt{B{C}^{2}+F{C}^{2}}$=10(m),
∵AD∥BE,DE∥AC,
∴四边形ADEF是平行四边形,
∴AD=EF,
∴AD+EB=EF+EB=BF=10m;
(2)∵四边形ADEF是平行四边形,
∴DE=AF=AC-FC=12-8=4(m).
点评 此题考查了坡度坡角问题以及平行四边形的性质与判定.注意准确作出辅助线是解此题的关键.

练习册系列答案
相关题目
12.a为有理数,下列说法中正确的是( )
| A. | -a一定是负数 | B. | -a2一定是负数 | C. | (-a)3一定是负数 | D. | |a|一定不是负数 |
9.若a与2014的互为倒数,则a的值是( )
| A. | -2014 | B. | 2014 | C. | -$\frac{1}{2014}$ | D. | $\frac{1}{2014}$ |
16. 如图,一圆弧形钢梁的拱高CD为8m,跨径AB为40m,则这钢梁圆弧的半径是( )
如图,一圆弧形钢梁的拱高CD为8m,跨径AB为40m,则这钢梁圆弧的半径是( )
 如图,一圆弧形钢梁的拱高CD为8m,跨径AB为40m,则这钢梁圆弧的半径是( )
如图,一圆弧形钢梁的拱高CD为8m,跨径AB为40m,则这钢梁圆弧的半径是( )| A. | 28m | B. | 29m | C. | 30m | D. | 31m |
13.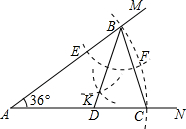 如图,小明作图如下:
如图,小明作图如下:
(1)用量角器作∠MAN=36°;
(2)以A为圆心适当长为半径作圆弧,分别交AM,AN于B,C两点,连结BC;
(3)以B为圆心适当长为半径作圆弧,分别交AB,BC于E,F两点,再分别以E,F为圆心大于$\frac{1}{2}$EF长为半径作圆弧,两条圆弧交于点K,连结BK并延长交AC于点D.
若AD=a,则由以上作图可得AB为( )
 如图,小明作图如下:
如图,小明作图如下:(1)用量角器作∠MAN=36°;
(2)以A为圆心适当长为半径作圆弧,分别交AM,AN于B,C两点,连结BC;
(3)以B为圆心适当长为半径作圆弧,分别交AB,BC于E,F两点,再分别以E,F为圆心大于$\frac{1}{2}$EF长为半径作圆弧,两条圆弧交于点K,连结BK并延长交AC于点D.
若AD=a,则由以上作图可得AB为( )
| A. | $\frac{\sqrt{5}-1}{2}$a | B. | $\frac{3-\sqrt{5}}{2}$a | C. | $\frac{\sqrt{5}+1}{2}a$ | D. | $\frac{3+\sqrt{5}}{2}$a |
