题目内容
10.若a、b均为正整数,且a>$\sqrt{11}$,b>$\root{3}{9}$,则a+b的最小值是( )| A. | 6 | B. | 7 | C. | 8 | D. | 9 |
分析 先根据平方根和立方根估算出a,b的范围,再确定a,b的最小正整数值,即可解答.
解答 解:∵9<11<16,
∴3<$\sqrt{11}$<4,
而a>$\sqrt{11}$,
∴正整数a的最小值为4,
∵8<9<27,
∴2<$\root{3}{9}$<3,
而b$>\root{3}{9}$,
∴正整数b的最小值为3,
∴a+b的最小值是3+4=7.
故选:B.
点评 本题考查了立方根、估算无理数的大小:利用完全平方数和算术平方根对无理数的大小进行估算.也考查了算术平方根和立方根.

练习册系列答案
 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案
相关题目
15.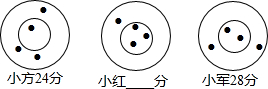 小方、小红和小军三人玩飞镖游戏,各投四支飞镖,规定在同一圆环内得分相同,中靶和得分情况如图,则小红的得分是( )
小方、小红和小军三人玩飞镖游戏,各投四支飞镖,规定在同一圆环内得分相同,中靶和得分情况如图,则小红的得分是( )
 小方、小红和小军三人玩飞镖游戏,各投四支飞镖,规定在同一圆环内得分相同,中靶和得分情况如图,则小红的得分是( )
小方、小红和小军三人玩飞镖游戏,各投四支飞镖,规定在同一圆环内得分相同,中靶和得分情况如图,则小红的得分是( )| A. | 30分 | B. | 32分 | C. | 33分 | D. | 34分 |
2.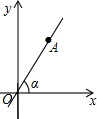 如图,在平面直角坐标系中,直线OA过点A(3,4),则tanα的值是( )
如图,在平面直角坐标系中,直线OA过点A(3,4),则tanα的值是( )
 如图,在平面直角坐标系中,直线OA过点A(3,4),则tanα的值是( )
如图,在平面直角坐标系中,直线OA过点A(3,4),则tanα的值是( )| A. | $\frac{3}{5}$ | B. | $\frac{4}{5}$ | C. | $\frac{3}{4}$ | D. | $\frac{4}{3}$ |
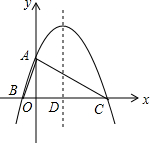 如图,已知二次函数y=ax2+bx+4的图象与y轴交于点A,与x轴交于B(-2,0)、C(8,0)两点,其对称轴与x轴交于点D,连接AC、AB.
如图,已知二次函数y=ax2+bx+4的图象与y轴交于点A,与x轴交于B(-2,0)、C(8,0)两点,其对称轴与x轴交于点D,连接AC、AB.
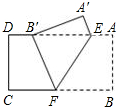 如图,把矩形纸片ABCD沿EF折叠,使点B落在边AD上,的点B′处,点A落在点A′处,若AE=6,BF=10,则AB=8.
如图,把矩形纸片ABCD沿EF折叠,使点B落在边AD上,的点B′处,点A落在点A′处,若AE=6,BF=10,则AB=8.