题目内容
17.先化简,再求值:$\frac{2}{a+1}-\frac{a-2}{{{a^2}-1}}÷\frac{{{a^2}-2a}}{{{a^2}-2a+1}}$,其中a=cos45°.分析 原式第二项利用除法法则变形,约分后两项通分并利用同分母分式的减法法则计算得到最简结果,把a的值代入计算即可求出值.
解答 解:原式=$\frac{2}{a+1}$-$\frac{a-2}{(a+1)(a-1)}$•$\frac{(a-1)^{2}}{a(a-2)}$=$\frac{2}{a+1}$-$\frac{a-1}{a(a+1)}$=$\frac{2a-a+1}{a(a+1)}$=$\frac{a+1}{a(a+1)}$=$\frac{1}{a}$,
当a=cos45°=$\frac{\sqrt{2}}{2}$时,原式=$\sqrt{2}$.
点评 此题考查了分式的化简求值,以及特殊角的三角函数值,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
8.设A(-2,y1),B(-1,y2),C(1,y3)是抛物线y=(x+1)2-m上的三点,则y1,y2,y3的大小关系为( )
| A. | y1>y2>y3 | B. | y1>y3>y2 | C. | y3>y2>y1 | D. | y3>y1>y2 |
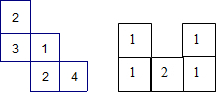 如图,这是一个由小立方块塔成的几何体从上面看到的形状图,小正方形中的数字表示该位置的小立方块的个数.请你画出它从正面、从左面看到的形状图.
如图,这是一个由小立方块塔成的几何体从上面看到的形状图,小正方形中的数字表示该位置的小立方块的个数.请你画出它从正面、从左面看到的形状图. 如图,AB是⊙O的直径,AC=15,AB=17,那么⊙O的弦BC=8.
如图,AB是⊙O的直径,AC=15,AB=17,那么⊙O的弦BC=8.