题目内容
17.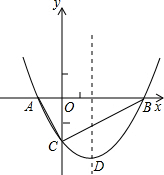 如图,抛物线y=$\frac{1}{2}$x2+bx-2与x轴交于A、B两点,与y轴交于C点,且A(-1,0).
如图,抛物线y=$\frac{1}{2}$x2+bx-2与x轴交于A、B两点,与y轴交于C点,且A(-1,0).(1)求抛物线的解析式及顶点D的坐标;
(2)求抛物线与x轴另一个交点B的坐标,并观察图象直接写出当x为何值时y>0?
(3)当-2≤x≤2时,求y的取值范围.
分析 (1)把A点坐标代入y=$\frac{1}{2}$x2+bx-2求出b=-$\frac{3}{2}$,从而得到抛物线解析式,然后把一般式通过配方化为顶点式即可得到顶点D的坐标;
(2)通过解方程x2-$\frac{3}{2}$x-2=0可得到B点坐标,然后观察函数图象,写出抛物线在x轴上方所对应的自变量的范围即可;
(3)先分别计算出当x=-2和x=2所对应的函数值,由于x=$\frac{3}{2}$时,y的最小值为-$\frac{25}{8}$,于是得到y的取值范围为-$\frac{25}{8}$≤y≤3.
解答 解:(1)把A(-1,0)代入y=$\frac{1}{2}$x2+bx-2得$\frac{1}{2}$-b-2=0,解得b=-$\frac{3}{2}$,
所以抛物线解析式为y=$\frac{1}{2}$x2-$\frac{3}{2}$x-2,
因为y=$\frac{1}{2}$x2-$\frac{3}{2}$x-2=$\frac{1}{2}$(x-$\frac{3}{2}$)2-$\frac{25}{8}$,
所以顶点D的坐标为($\frac{3}{2}$,-$\frac{25}{8}$);
(2)当y=0时,$\frac{1}{2}$x2-$\frac{3}{2}$x-2=0,
整理得x2-3x-4=0,解得x1=-1,x2=4,
所以B点坐标为(4,0),
当x<-1或x>4时,y>0;
(3)当x=-2时,y=$\frac{1}{2}$x2-$\frac{3}{2}$x-2=3;当x=2时,y=$\frac{1}{2}$x2-$\frac{3}{2}$x-2=-3,
所以当-2≤x≤2时,y的取值范围为-$\frac{25}{8}$≤y≤3.
点评 本题考查了抛物线与x轴的交点:把求二次函数y=ax2+bx+c(a,b,c是常数,a≠0)与x轴的交点坐标问题转化为解关于x的一元二次方程.也考查了二次函数与不等式.解决(3)小题的关键是x=$\frac{3}{2}$时,y的最小值为-$\frac{25}{8}$.

| A. | -a一定是负数 | B. | -a2一定是负数 | C. | (-a)3一定是负数 | D. | |a|一定不是负数 |
| A. | -2014 | B. | 2014 | C. | -$\frac{1}{2014}$ | D. | $\frac{1}{2014}$ |
| A. | y1>y2 | B. | y1<y2 | C. | y1=y2 | D. | 无法确定 |
 如图,将长方形ABCD边AD沿折痕AE折叠,使点D落在BC上的点F处,已知AB=6,△ABF的面积是24,求DE的长.
如图,将长方形ABCD边AD沿折痕AE折叠,使点D落在BC上的点F处,已知AB=6,△ABF的面积是24,求DE的长.