题目内容
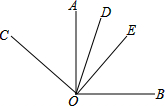 如图,OA⊥OB,∠AOC=
如图,OA⊥OB,∠AOC=| 1 |
| 2 |
考点:垂线,角平分线的定义
专题:
分析:根据垂线的定义,可得∠AOB的度数,根据∠AOC=
∠AOB,可得∠AOC的度数,根据角的和差,可得∠BOC,根据角平分线的性质,可得∠COD,根据角的和差,可得∠AOD,根据角平分线的性质,可得∠AOE,根据角的和差,可得答案.
| 1 |
| 2 |
解答:解:如图:
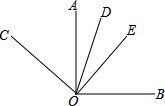 ,
,
由OA⊥OB,得∠AOB=90°,
由∠AOC=
∠AOB,得∠AOC=
∠AOB=
×90°=45°.
由角的和差,得∠BOC=∠AOB+AOC=90°+45°=135°,
由OD平分∠BOC,得∠COD=∠BOD=
∠BOC=
×135°=67.5°,
由角的和差,得∠AOD=∠COD-∠AOC=67.5°-45°=22.5°,
由OE平分∠AOB,得∠AOE=
∠AOB=
×90°=45°,
由角的和差,得∠EOD=∠AOE-∠AOD=45°-22.5=22.5°.
 ,
,由OA⊥OB,得∠AOB=90°,
由∠AOC=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
由角的和差,得∠BOC=∠AOB+AOC=90°+45°=135°,
由OD平分∠BOC,得∠COD=∠BOD=
| 1 |
| 2 |
| 1 |
| 2 |
由角的和差,得∠AOD=∠COD-∠AOC=67.5°-45°=22.5°,
由OE平分∠AOB,得∠AOE=
| 1 |
| 2 |
| 1 |
| 2 |
由角的和差,得∠EOD=∠AOE-∠AOD=45°-22.5=22.5°.
点评:本题考查了垂线,利用了垂线的定义,角的和差,角平分线的性质.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案
相关题目
 如图,两棵树AB、CD的高分别是6m、9m,它们根部的距离AC=6m,小强从点G出出发沿着正对这两棵树的方向前进,小强的眼睛与地面的距离为1.6m,当小强与树AB的距离为多少时,他看不见树顶D?
如图,两棵树AB、CD的高分别是6m、9m,它们根部的距离AC=6m,小强从点G出出发沿着正对这两棵树的方向前进,小强的眼睛与地面的距离为1.6m,当小强与树AB的距离为多少时,他看不见树顶D? 如图所示,过直线l外一点C画直线l的垂线,请你根据作图痕迹,叙述画图过程.
如图所示,过直线l外一点C画直线l的垂线,请你根据作图痕迹,叙述画图过程.