��Ŀ����
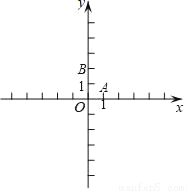
��֪��ƽ��ֱ������ϵxOy����ͼ���У���֪������y=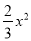 +bx+c�㾭��A��1��0����B��0��2����
+bx+c�㾭��A��1��0����B��0��2����
��1����������ߵı���ʽ��
��2����������ߵĶԳ�����x��Ľ���ΪC�����������ڵĵ�D�ڸ������ߵĶԳ����ϣ�����Ե�A��C��D����ɵ����������AOB���ƣ����D�����ꣻ
��3�����E�ڸ������ߵĶԳ����ϣ�������������1������AE��BE����sin��ABE��
��ϰ��ϵ�д�
�����Ŀ


 �Ƕ�Ԫһ�η���
�Ƕ�Ԫһ�η���

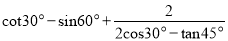 .
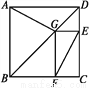
.
 ������ѡһ����ϲ������
������ѡһ����ϲ������ ������ֵ��
������ֵ��