题目内容
若a-b+c=0,且a≠0,则二次函数y=ax2+bx+c必经过点 .
【答案】分析:根据a-b+c=0和二次函数y=ax2+bx+c解析式,对比可得当x=-1,y=0时,刚好满足a-b+c=0,所以函数必过点(-1,0).
解答:解:∵二次函数解析式为y=ax2+bx+c,
又∵a-b+c=0,且a≠0,
∴对比可得,当x=-1,y=0时,解析式刚好满足已知条件a-b+c=0,
∴二次函数必过点(-1,0).
点评:本题考查二次函数图象上点的坐标特征,需要认真观察和变向思维.
解答:解:∵二次函数解析式为y=ax2+bx+c,
又∵a-b+c=0,且a≠0,
∴对比可得,当x=-1,y=0时,解析式刚好满足已知条件a-b+c=0,
∴二次函数必过点(-1,0).
点评:本题考查二次函数图象上点的坐标特征,需要认真观察和变向思维.

练习册系列答案
相关题目
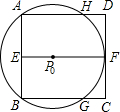 装置)P到达点P0处时,⊙P0与BC、EF、AD分别交于G、F、H点.
装置)P到达点P0处时,⊙P0与BC、EF、AD分别交于G、F、H点.
 (2013•丰台区一模)如图,在平面直角坐标系xOy中,⊙C的圆心坐标为(-2,-2),半径为
(2013•丰台区一模)如图,在平面直角坐标系xOy中,⊙C的圆心坐标为(-2,-2),半径为 C于E,过O作OD∥BC交⊙O于D,连接AE、AD、DC.
C于E,过O作OD∥BC交⊙O于D,连接AE、AD、DC.