题目内容
9.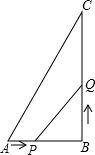 如图,在△ABC中∠B=90°,AB=6cm,BC=8cm,点P从点A开始沿AB边向点B以1cm/s的速度移动,与此同时,点Q从点B开始沿BC边向点C以2cm/s的速度移动.经过2或4s,S△BPQ=8;△BPQ的面积的变化趋势是先增大后减小(或者:符合S=-(t-3)2+9),△BPQ的面积的最大值为9cm2.
如图,在△ABC中∠B=90°,AB=6cm,BC=8cm,点P从点A开始沿AB边向点B以1cm/s的速度移动,与此同时,点Q从点B开始沿BC边向点C以2cm/s的速度移动.经过2或4s,S△BPQ=8;△BPQ的面积的变化趋势是先增大后减小(或者:符合S=-(t-3)2+9),△BPQ的面积的最大值为9cm2.
分析 设出运动所求的时间,可将BP和BQ的长表示出来,代入三角形面积公式,列出等式,可将时间求出;结合函数图象的性质得到面积变化趋势,由二次函数解析式来求其最值.
解答 解:设运动时间为t(s),得
$\frac{1}{2}$•2t(6-t)=8,
解得t1=2,t2=4.
故经过2或4秒,△PBQ的面积等于8cm2;
因为S=$\frac{1}{2}$•2t(6-t)=-(t-3)2+9,即S=-(t-3)2+9,
所以抛物线的顶点坐标是(3,9),且抛物线开口方向向下,
所以△BPQ的面积的变化趋势是 先增大后减小(或者:符合S=-(t-3)2+9),且当t=3时,△BPQ的面积的最大值为 9cm2.
故答案是:2或4;先增大后减小(或者:符合S=-(t-3)2+9); 9cm2.
点评 本题考查了一元二次方程的应用.关键是用含时间的代数式准确表示BP和BQ的长度,再根据三角形的面积公式列出一元二次方程,进行求解.

练习册系列答案
 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案
相关题目
19.如果关于x的二次三项式x2+bx+9是完全平方式,那么b的值为( )
| A. | 3 | B. | ±3 | C. | 6 | D. | ±6 |
 如图,在四边形ABCD中,AD∥BC,∠B=90°,AD=8cm,BC=10cm,AB=6cm,点Q从点A出发以1cm/s的速度向点D运动,点P从点B出发以2cm/s的速度向点C运动,P、Q两点同时出发,当点P到达点C时,两点同时停止运动.若设运动时间为t(s)
如图,在四边形ABCD中,AD∥BC,∠B=90°,AD=8cm,BC=10cm,AB=6cm,点Q从点A出发以1cm/s的速度向点D运动,点P从点B出发以2cm/s的速度向点C运动,P、Q两点同时出发,当点P到达点C时,两点同时停止运动.若设运动时间为t(s)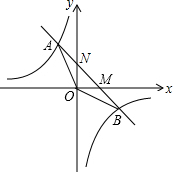 如图,已知一次函数y=kx+b的图象与反比例函数y=-$\frac{8}{x}$的图象交于A,B两点,且点A的横坐标和点B的纵坐标都是-2,求:
如图,已知一次函数y=kx+b的图象与反比例函数y=-$\frac{8}{x}$的图象交于A,B两点,且点A的横坐标和点B的纵坐标都是-2,求: