题目内容
如图，在?ABCD中，E在DC上，若DE：EC=1：2，则BF：EF=考点：平行四边形的性质,相似三角形的判定与性质
专题：
分析：由DE、EC的比例关系式，可求出EC、DC的比例关系；由于平行四边形的对边相等，即可得出EC、AB的比例关系，易证得△EFC∽△BFA，可根据相似三角形的对应边成比例求出BF、EF的比例关系．
解答：解：∵DE：EC=1：2，
∴EC：DC=2：3，；
∵四边形ABCD是平行四边形，
∴AB∥CD，AB=CD，
∴△ABF∽△CEF，
∴BF：EF=AB：EC，
∵AB：EC=CD：EC=3：2，
∴BF：FE=3：2，
故答案为：3：2．
∴EC：DC=2：3，；
∵四边形ABCD是平行四边形，
∴AB∥CD，AB=CD，
∴△ABF∽△CEF，
∴BF：EF=AB：EC，
∵AB：EC=CD：EC=3：2，
∴BF：FE=3：2，
故答案为：3：2．
点评：此题主要考查的是平行四边形的性质以及相似三角形的判定和性质．
练习册系列答案
综合自测系列答案
相关题目
如图，AC、BD相交于点O，∠A=∠D，请补充一个条件，使△AOB≌△DOC，你补充的条件是
如图，直线a、b被直线c所截，a∥b，∠1+∠2的度数是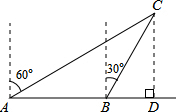
如图，一渔船由西往东航行，在A点测得海岛C位于北偏东60°的方向，前进20海里到达B点，此时，测得海岛C位于北偏东30°的方向，则海岛C到航线AB的距离CD等于
