题目内容
解方程：
（y+1）+
（y+2）+
（y+3）+…+
（y+2013）=2013．
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 2014 |
考点：解一元一次方程
专题：
分析：将原方程拆项变形为：（
+
+
+…+
）y+（
+
+
+…+
）=2013，进一步移项合并即可得到：（
+
+
+…+
）y=
+
+
+
，从而可求出y的值．
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 2014 |
| 1 |
| 2 |
| 2 |
| 3 |
| 3 |
| 4 |
| 2013 |
| 2014 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 2014 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 4 |
| 2013 |
| 2014 |
解答：解：
（y+1）+
（y+2）+
（y+3）+…+
（y+2013）=2013．
原方程可变形为：
（
+
+
+…+
）y+（
+
+
+…+
）=2013，
移项，合并得：
（
+
+
+…+
）y=
+
+
+
，
系数化为1得：
y=1．
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 2014 |
原方程可变形为：
（
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 2014 |
| 1 |
| 2 |
| 2 |
| 3 |
| 3 |
| 4 |
| 2013 |
| 2014 |
移项，合并得：
（
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 2014 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 4 |
| 2013 |
| 2014 |
系数化为1得：
y=1．
点评：此题考查了一元一次方程的解法，解题的关键是：将原方程拆项变形．
练习册系列答案
小天才课时作业系列答案
一课四练系列答案
黄冈小状元满分冲刺微测验系列答案
新辅教导学系列答案
相关题目
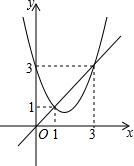函数y1=ax2+bx+c与y2=x的图象如图所示，当y1＜y2时，自变量x的取值范围是（ ）| A、1＜x＜3 | B、x＜1 |
| C、x＞3 | D、x＜1或x＞3 |
反比例函数y=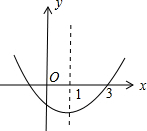
如图，二次函数y=ax2+bx+c的图象开口向上，对称轴为直线x=1，且图象经过点（3，0），下列结论中，正确的是
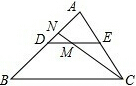如图，在△ABC中，DE∥BC，M为DE中点，CM的延长线交AB于N，若AD：AB=2：3，求ND：BD．
如图，Rt△ABC中，∠ABC=90°，BD⊥AB于D，且∠A=60°，BD=4cm，则BC=