题目内容
已知二次函数y=ax2+bx+c（a≠0）的图象与x轴交于A（1，0），B（3，0）两点，与y轴交于点C（0，3），求二次函数的解析式．
考点：待定系数法求二次函数解析式
专题：
分析：把点A、B、C的坐标代入函数解析式，解方程组求出a、b、c的值，即可得解．
解答：解：将A（1，0），B（3，0），C（0，3）代入函数解析式得，
，
解得
．
所以二次函数的解析式为y=x2-4x+3．
|
解得
|
所以二次函数的解析式为y=x2-4x+3．
点评：本题考查了待定系数法求二次函数解析式，待定系数法是求函数解析式常用的方法，需熟练掌握，难点在于解三元一次方程组．
练习册系列答案
相关题目
已知|x-3|+|5-x|=2，则化简
+
的结果是（ ）
| (1-x)2 |
| (5-x)2 |
| A、4 | B、6-2x |
| C、-4 | D、2x-6 |
下面各组数不是方程x-y=3的解的是（ ）
A、
| |||||
B、
| |||||
C、
| |||||
D、
|
下列各式中，代数式的个数有（ ）
①a；②ab=ba；③0；④2x=6；⑤mx-ny；⑥
；⑦m2-
．
①a；②ab=ba；③0；④2x=6；⑤mx-ny；⑥
| a |
| b |
| 1 |
| n |
| A、2个 | B、3个 | C、4个 | D、5个 |
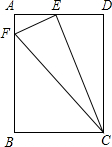已知：如图，在矩形ABCD中，E为AD的中点，EF⊥EC交AB于F，连接FC．（AB＞AE）