题目内容
9. 如图,在△ABC中,∠BAC=90°,AD⊥BC于D,BF平分∠ABC交AD于E点,交AC于F点.求证:∠AEF=∠AFE.
如图,在△ABC中,∠BAC=90°,AD⊥BC于D,BF平分∠ABC交AD于E点,交AC于F点.求证:∠AEF=∠AFE.
分析 由在△ABC中,∠BAC=90°,AD⊥BC,易得∠BAD=∠C,又由BF平分∠ABC,∠AEF=∠ABE+∠BAD,∠AFE=∠CBF+∠C,即可证得∠AEF=∠AFE,继而证得△AEF为等腰三角形.
解答 证明:∵在△ABC中,∠BAC=90°,AD⊥BC,
∴∠BAD+∠CAD=90°,∠CAD+∠C=90°,
∴∠BAD=∠C,
∵BF平分∠ABC,
∴∠ABE=∠CBF,
∵∠AEF=∠ABE+∠BAD,∠AFE=∠CBF+∠C,
∴∠AEF=∠AFE,
∴AF=AE,即△AEF为等腰三角形.
点评 此题考查了等腰三角形的判定、直角三角形的性质以及三角形外角的性质.此题难度适中,注意掌握数形结合思想的应用.

练习册系列答案
 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案
相关题目
17.已知x=1是关于x的方程2x-a=0的解,则a的值是( )
| A. | -5 | B. | 5 | C. | 7 | D. | 2 |
4.下列各组长度的线段能构成三角形的是( )
| A. | 1.5cm,3.9cm,2.3cm | B. | 3.5cm,7.1cm,3.6cm | ||
| C. | 6cm,1cm,6cm | D. | 4cm,10cm,4cm |
14.一个多边形的每个外角都是45°,那么这个多边形的内角和等于( )
| A. | 720° | B. | 900° | C. | 675° | D. | 1080° |
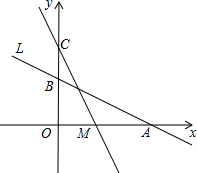 如图,直线L:y=-$\frac{1}{2}$x+2与x轴、y轴分别交于A、B两点,在y轴上有一点C(0,4),动点M从A点以每秒1个单位的速度沿x轴向左移动.
如图,直线L:y=-$\frac{1}{2}$x+2与x轴、y轴分别交于A、B两点,在y轴上有一点C(0,4),动点M从A点以每秒1个单位的速度沿x轴向左移动. 如图所示,根据数轴上各点的位置,写出它们所表示的数.
如图所示,根据数轴上各点的位置,写出它们所表示的数.