题目内容
1.阅读下列材料:∵$\sqrt{4}<\sqrt{7}<\sqrt{9}$,即2$<\sqrt{7}<3$,
∴$\sqrt{7}$的整数部分为2,小数部分为($\sqrt{7}-2$).
请根据材料提示,进行解答:
(1)$\sqrt{5}$的整数部分是2.
(2)如果$\sqrt{5}$的小数部分为a,$\sqrt{13}$的整数部分为b,求a+b-$\sqrt{5}$的值.
分析 (1)利用例题结合$\sqrt{4}$<$\sqrt{5}$<$\sqrt{9}$,进而得出答案;
(2)利用例题结合$\sqrt{9}$<$\sqrt{13}$<$\sqrt{16}$,进而得出答案.
解答 解:(1)∵$\sqrt{4}$<$\sqrt{5}$<$\sqrt{9}$,即2<$\sqrt{5}$<3,
∴$\sqrt{5}$的整数部分为2,
故答案为:2;
(2)由(1)得,$\sqrt{5}$的小数部分为:a=($\sqrt{5}$-2),
∵$\sqrt{9}$<$\sqrt{13}$<$\sqrt{16}$,即3<$\sqrt{13}$<4,
∴$\sqrt{13}$的整数部分为b=3,
则a+b-$\sqrt{5}$=$\sqrt{5}$-2+3-$\sqrt{5}$=1.
点评 此题主要考查了估算无理数的大小,正确估计出$\sqrt{5}$,$\sqrt{13}$最接近的有理数是解题关键.

练习册系列答案
相关题目
11.如果x=$\frac{1}{2}$是关于x的方程4x+m=3的解,那么m的值是( )
| A. | 1 | B. | $\frac{1}{2}$ | C. | -1 | D. | $-\frac{1}{2}$ |




 如图,已知∠1=∠2,要得到△ABD≌△ACD,还需补充一个条件,则这个条件可以是AB=AC(答案不唯一).
如图,已知∠1=∠2,要得到△ABD≌△ACD,还需补充一个条件,则这个条件可以是AB=AC(答案不唯一).
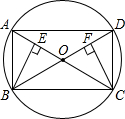 如图,在⊙O中,AC与BD是圆的直径,BE⊥AC,CF⊥BD,垂足分别为E、F
如图,在⊙O中,AC与BD是圆的直径,BE⊥AC,CF⊥BD,垂足分别为E、F 的值为零;当y__________时,分式
的值为零;当y__________时,分式 的值为负.
的值为负.