题目内容
19.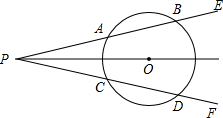 如图所示,点O是∠EPF平分线上的一点,以点O为圆心的圆与角的两边分别交于点A、B和C、D.
如图所示,点O是∠EPF平分线上的一点,以点O为圆心的圆与角的两边分别交于点A、B和C、D.(1)求证:AB=CD;
(2)若角的顶点P在圆上或在圆内,(1)的结论还成立吗?若不成立,请说明理由;若成立,请加以证明.
分析 (1)如图1,作辅助线;由角平分线的性质得到OM=ON;由垂径定理得到AB=CD,即可解决问题.
(2)如图3,作辅助线;类似(1)中的证明方法,由角平分线的性质得到OM=ON;由垂径定理得到AB=CD,即可解决问题
解答 
 解:(1)如图1,过点O作OM⊥AB,
解:(1)如图1,过点O作OM⊥AB,
ON⊥CD;
∵PO平分∠EPF,
∴OM=ON,
∴AB=CD(垂径定理的推论).
(2)如图2或图3,点P分别在⊙O上或⊙O内,(1)中的结论仍然成立;仅以图3为例证明如下:
如图3, 过点O作OM⊥AB、ON⊥CD;
过点O作OM⊥AB、ON⊥CD;
∵PO平分∠EPF,
∴OM=ON,
∴AB=CD(垂径定理的推论).
点评 该题主要考查了垂径定理、角平分线的性质等几何知识点及其应用问题;应牢固掌握垂径定理、角平分线的性质等几何知识点,这是灵活运用、解题的基础和关键.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
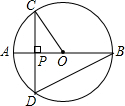 已知AB是⊙O的直径,弦CD⊥AB,垂足为P,
已知AB是⊙O的直径,弦CD⊥AB,垂足为P, 如图,直线1与反比例函数y=$\frac{2}{x}$的图象在第一象限内交于A,B两点,交x轴于点C,若AB:BC=(m-1):1(m>1),则△OAB的面积(用m表示)为$\frac{{m}^{2}-1}{m}$.
如图,直线1与反比例函数y=$\frac{2}{x}$的图象在第一象限内交于A,B两点,交x轴于点C,若AB:BC=(m-1):1(m>1),则△OAB的面积(用m表示)为$\frac{{m}^{2}-1}{m}$.
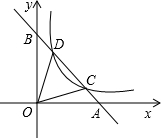 如图,直线AB过点A(8,0)、B(0,6).反比例函数$y=\frac{p}{x}$(p>0)的图象与直线AB交于C、D两点,连接OC、OD.
如图,直线AB过点A(8,0)、B(0,6).反比例函数$y=\frac{p}{x}$(p>0)的图象与直线AB交于C、D两点,连接OC、OD.