题目内容
若方程组 的解为
的解为 ,
,
求:(1)

(2)
 .
.
【答案】分析:利用代入消元法克得到x2+(x-6)2=34,整理得x2-6x+1=0,根据方程组的解的定义和根与系数的关系得到x1+x2=6,x1•x2=1,则y1+y2=x1+x2-12=6-12=-6,
y1,•y2=x1•x2-6(x1+x2)+36=1-6×6+36=1.
(1)变形 得到(x1+x2)2-2x1•x2,然后利用整体思想计算;
得到(x1+x2)2-2x1•x2,然后利用整体思想计算;
(2) +
+ 得到
得到 ,然后利用整体思想计算.
,然后利用整体思想计算.
解答:解: ,
,
由②得y=x-6③,
把③代入①得x2+(x-6)2=34,
整理得x2-6x+1=0,
根据题意得x1+x2=6,x1•x2=1,
(1)
=(x1+x2)2-2x1•x2
=36-2
=34;
(2)∵y=x-6,
∴y1=x1-6,y2=x2-6,
∴y1+y2=x1+x2-12=6-12=-6,
y1,•y2=x1•x2-6(x1+x2)+36=1-6×6+36=1,
∴ +
+ =
= =
= =-6.
=-6.
点评:本题考查了一元二次方程ax2+bx+c=0(a≠0)的根与系数的关系:若方程两个为x1,x2,则x1+x2=- ,x1•x2=
,x1•x2= .也考查了代数式的变形能力.
.也考查了代数式的变形能力.
y1,•y2=x1•x2-6(x1+x2)+36=1-6×6+36=1.
(1)变形
 得到(x1+x2)2-2x1•x2,然后利用整体思想计算;
得到(x1+x2)2-2x1•x2,然后利用整体思想计算;(2)
 +
+ 得到
得到 ,然后利用整体思想计算.
,然后利用整体思想计算.解答:解:
 ,
,由②得y=x-6③,
把③代入①得x2+(x-6)2=34,
整理得x2-6x+1=0,
根据题意得x1+x2=6,x1•x2=1,
(1)

=(x1+x2)2-2x1•x2
=36-2
=34;
(2)∵y=x-6,
∴y1=x1-6,y2=x2-6,
∴y1+y2=x1+x2-12=6-12=-6,
y1,•y2=x1•x2-6(x1+x2)+36=1-6×6+36=1,
∴
 +
+ =
= =
= =-6.
=-6.点评:本题考查了一元二次方程ax2+bx+c=0(a≠0)的根与系数的关系:若方程两个为x1,x2,则x1+x2=-
 ,x1•x2=
,x1•x2= .也考查了代数式的变形能力.
.也考查了代数式的变形能力. 
练习册系列答案
相关题目

 的解为
的解为 ,求方程组②
,求方程组② 的解时,令方程组②中的x+2=a,y-1=b,则方程组②就转化为方程组①,所以可得x+2=8.3,y-1=1.2,故方程组②的解为________.
的解时,令方程组②中的x+2=a,y-1=b,则方程组②就转化为方程组①,所以可得x+2=8.3,y-1=1.2,故方程组②的解为________. 的解是
的解是 ,求关于x,y的二元一次方程组.
,求关于x,y的二元一次方程组.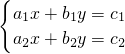 的解为
的解为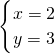 .求方程组
.求方程组 的解.
的解. 的解为
的解为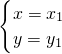 ,
,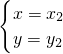

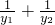 .
.