题目内容
8.若2(x2+3)的值与3(1-x2)的值互为相反数,求$\frac{3+x}{{x}^{2}}$的值.分析 根据相反数对应得到2(x2+3)+3(1-x2)=0,整理得x2=9,再利用直接开平方法解方程,然后把x的值分别代入$\frac{3+x}{{x}^{2}}$中计算即可.
解答 解:根据题意得2(x2+3)+3(1-x2)=0,
整理得x2=9,
所以x1=3,x2=-3
当x=3时,$\frac{3+x}{{x}^{2}}$=$\frac{3+3}{9}$=$\frac{2}{3}$,
当x=-3时,$\frac{3+x}{{x}^{2}}$=$\frac{3-3}{9}$=0.
点评 本题考查了解一元二次方程-直接开平方法:形如x2=p或(nx+m)2=p(p≥0)的一元二次方程可采用直接开平方的方法解一元二次方程.

练习册系列答案
相关题目
16. 如图,在平行四边形纸片ABCD中,BC=4$\sqrt{3}$,将纸片沿对角线AC对折,BC边与AD边交于点E,此时,△CDE恰为等边三角形,则重叠面积为( )
如图,在平行四边形纸片ABCD中,BC=4$\sqrt{3}$,将纸片沿对角线AC对折,BC边与AD边交于点E,此时,△CDE恰为等边三角形,则重叠面积为( )
 如图,在平行四边形纸片ABCD中,BC=4$\sqrt{3}$,将纸片沿对角线AC对折,BC边与AD边交于点E,此时,△CDE恰为等边三角形,则重叠面积为( )
如图,在平行四边形纸片ABCD中,BC=4$\sqrt{3}$,将纸片沿对角线AC对折,BC边与AD边交于点E,此时,△CDE恰为等边三角形,则重叠面积为( )| A. | $\sqrt{3}$ | B. | 2$\sqrt{3}$ | C. | 3$\sqrt{3}$ | D. | 4$\sqrt{3}$ |
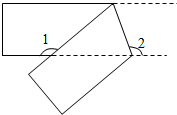 将一个宽度相等的纸条按如图所示方式折叠,如果∠1=138°,那么∠2=111°.
将一个宽度相等的纸条按如图所示方式折叠,如果∠1=138°,那么∠2=111°.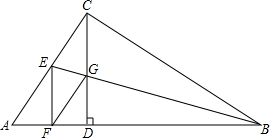 如图,已知在Rt△ABC中,CD是斜边AB上的高,∠ABC的平分线BE交CD于点G,交AC于点E,GF∥AC交AB于点F.求证:EF⊥AB.
如图,已知在Rt△ABC中,CD是斜边AB上的高,∠ABC的平分线BE交CD于点G,交AC于点E,GF∥AC交AB于点F.求证:EF⊥AB.