题目内容
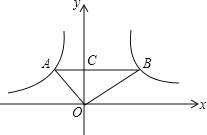
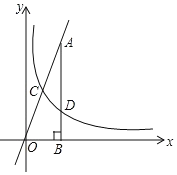
【题目】如图,反比例函数![]() 的图象与直线y=3x相交于点C,过直线上点A(1,3)作AB⊥x轴于点B,交反比例函数图象于点D,且AB=3BD.
的图象与直线y=3x相交于点C,过直线上点A(1,3)作AB⊥x轴于点B,交反比例函数图象于点D,且AB=3BD.
(1)求反比例函数的表达式;
(2)求点C的坐标;
(3)在y轴上确定一点M,使点M到C,D两点距离之和d=MC+MD最小,求点M的坐标.
【答案】(1)![]() ;(2)C(
;(2)C(![]() ,
,![]() );(3)M(0,
);(3)M(0,![]() )
)
【解析】
(1)由条件可求得D点坐标,则可求得反比例函数解析式;
(2)联立直线与反比例函数解析式可求得C点坐标;
(3)找C点关于y轴的对称点为C′,连接C′D交y轴于点,由对称的性质可知M点即为所求的点.
(1)∵A(1,3),AB⊥x轴于点D,
∴AB=3,OB=1,
∵AB=3BD,
∴BD=1,
∴D(1,1),
∵点D在反比例函数图象上,
∴1=![]() ,解得k=1,
,解得k=1,
∴反比例函数解析式为y=![]() ;
;
(2)联立直线与反比例函数解析式可得
 ,解得
,解得 或
或 ,
,
∵点C在第一象限,
∴C点坐标为:(![]() ,
,![]() );
);
(3)设点C关于y轴的对称点为C′,
∴C′(-![]() ,
,![]() ),
),
连接C′D交y轴于点M,
′
则MC=MC′,
∴d=MC+MD=MC′+MD=DC′,
∴点M即为满足条件的点,
设直线C′D解析式为y=mx+n,
把C′、D的坐标代入可得 ,解得
,解得 ,
,
∴直线C′D的解析式为y=(3-2![]() )x+(2
)x+(2![]() -2),
-2),
令x=0可得y=2![]() -2,
-2,
∴M(0,2![]() -2).
-2).

练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案
相关题目
【题目】二次函数![]() (
(![]() 是常数,
是常数,![]() )的自变量
)的自变量![]() 与函数值
与函数值![]() 的部分对应值如下表:
的部分对应值如下表:
| … |
|
| 0 | 1 | 2 | … |
| … |
|
|
|
|
| … |
且当![]() 时,与其对应的函数值
时,与其对应的函数值![]() .有下列结论:①
.有下列结论:①![]() ;②
;②![]() 和3是关于
和3是关于![]() 的方程
的方程![]() 的两个根;③
的两个根;③![]()
![]() .其中,正确结论的个数是( )
.其中,正确结论的个数是( )
A. 0B. 1C. 2D. 3