题目内容
证明：在任意给定的100个整数中，一定存在两个数，它们的和或差是100的倍数．
分析：我们可以把所有自然数按被100除所得的100种不同的余数0、1、2、3、4、5、6…分成100类，也就是100个抽屉．利用抽屉原理，即可证得：在任意给定的100个整数中，一定存在两个数，它们的和或差是100的倍数．
解答：解：我们可以把所有自然数按被100除所得的100种不同的余数0、1、2、3、4、5、6…分成100类，也就是100个抽屉．
任取100个整数，根据抽屉原理，
如果正好每个抽屉中都有一个数，则就能找到1+99=2+98=3+97=…=100的两个数，
除了上面的情况外，必有两个数在同一个抽屉中，也就是它们除以100的余数相同，因此这两个数的差一定是100的倍数．
∴在任意给定的100个整数中，一定存在两个数，它们的和或差是100的倍数．
任取100个整数，根据抽屉原理，
如果正好每个抽屉中都有一个数，则就能找到1+99=2+98=3+97=…=100的两个数，
除了上面的情况外，必有两个数在同一个抽屉中，也就是它们除以100的余数相同，因此这两个数的差一定是100的倍数．
∴在任意给定的100个整数中，一定存在两个数，它们的和或差是100的倍数．
点评：本题考查抽屉原理的应用，难度较大．解题时要注意合理的找到抽屉，利用抽屉原理解题是竞赛题中的常见题目，同学们应该掌握．
练习册系列答案
新思维假期作业暑假吉林大学出版社系列答案
蓝天教育暑假优化学习系列答案
相关题目
x+
，求A，B两点的坐标；
：
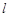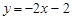上的点，过点P的另一条直线
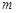交抛物线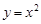
于A、B两点．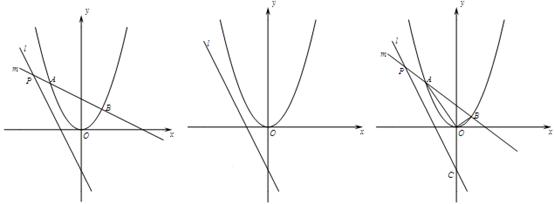
，求A、B两点的坐标；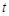 
），当PA＝AB时，请直接写出点A的坐标；
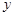轴于点C，若△AOB的外心在边AB上，且∠BPC＝∠OCP，求点P的坐标．