题目内容
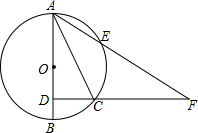 已知:如图,AB是⊙O的直径,点C为⊙O上一点,过点C作CD⊥AB于点D,CD=4,AD=8.点E为
已知:如图,AB是⊙O的直径,点C为⊙O上一点,过点C作CD⊥AB于点D,CD=4,AD=8.点E为 |
| AC |
(1)求⊙O的半径;
(2)求证:CA=CF.
考点:垂径定理,勾股定理,圆周角定理
专题:
分析:(1)连接OC,根据勾引股定理求出r的值即可;
(2)连接BE,先根据圆周角定理得出∠AEB=90°,再根据两角互余的性质得出∠B=∠F,根据点E为
的中点得出
=
,故∠CAE=∠B,∠CAE=∠F,由此可得出结论.
(2)连接BE,先根据圆周角定理得出∠AEB=90°,再根据两角互余的性质得出∠B=∠F,根据点E为
 |
| AC |
 |
| AE |
 |
| CE |
解答: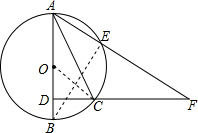 解:(1)连接OC,
解:(1)连接OC,
∵AD=8,
∴OD=8-r.
∵CD⊥AB,
∴根据勾股定理得出:OD2+CD2=OC2,则(8-r)2+42=r2,解的r=5;
(2)连接BE,
∵AB为直径,
∴∠AEB=90°,
∴∠B+∠BAE=90°.
又∵∠F+∠BAE=90°,
∴∠B=∠F.
∵点E为
的中点,
∴
=
,
∴∠CAE=∠B,
∴∠CAE=∠F,
∴AC=CF.
 解:(1)连接OC,
解:(1)连接OC,∵AD=8,
∴OD=8-r.
∵CD⊥AB,
∴根据勾股定理得出:OD2+CD2=OC2,则(8-r)2+42=r2,解的r=5;
(2)连接BE,
∵AB为直径,
∴∠AEB=90°,
∴∠B+∠BAE=90°.
又∵∠F+∠BAE=90°,
∴∠B=∠F.
∵点E为
 |
| AC |
∴
 |
| AE |
 |
| CE |
∴∠CAE=∠B,
∴∠CAE=∠F,
∴AC=CF.
点评:本题考查的是垂径定理,熟知平分弦的直径平分这条弦,并且平分弦所对的两条弧是解答此题的关键.

练习册系列答案
 一课一练课时达标系列答案
一课一练课时达标系列答案
相关题目
下列用等式的性质变形的方程,正确的是( )
A、
| ||||
B、
| ||||
| C、-2y=-5变成4y=10 | ||||
| D、3y-5=6变成3y=6-5 |
已知关于x的方程mx+2=2(m-x)的解满足2(x-
)-1=0,则m的值为( )
| 1 |
| 2 |
| A、-4 | B、-2 | C、2 | D、4 |
若y=(m2+m)xm2-2m-1-x+3是关于x的二次函数,则( )
| A、m=-1或m=3 |
| B、m≠-1且m≠0 |
| C、m=-1 |
| D、m=3 |
下列方程中是一元二次方程的是( )
A、x2+
| ||
| B、ax2+bx+c=0 | ||
| C、3x2-2xy-5y2=0 | ||
| D、(x-1)(x+2)=1 |
下列各式:
,
,
,
(x2+1),
,
中,是分式的共有( )
| a-b |
| 2 |
| x+3 |
| x |
| 5-y |
| π |
| ||
| 4 |
| a-b |
| a+b |
| 1 |
| m |
| A、4个 | B、3个 | C、2个 | D、1个 |