题目内容
如图,抛物线y=x2+mx+(m﹣1)与x轴交于点A(x1,0),B(x2,0),x1<x2,与y轴交于点C(0,c),且满足x12+x22+x1x2=7.

(1)求抛物线的解析式;
(2)在抛物线上能不能找到一点P,使∠POC=∠PCO?若能,请求出点P的坐标;若不能,请说明理由
1)抛物线的解析式是y=x2-2x-3;(2)能;点P的坐标是(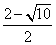 ,-
,-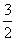 ),(
),( ,-
,-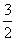 ).
).
【解析】(1)依题意:x1+x2=-m,x1x2=m-1,∵x12+x22+x1x2=7,∴( x1+x2)2-x1x2=7,
x1+x2)2-x1x2=7,
∴(-m)2-(m-1)=7,即m2-m-6=0,解得m1=-2,m2=3,∵c=m-1<0,∴m=3不合题意
∴m=-2抛物线的解析式是y=x2-2x-3;
(2)能
如图,设P是抛物线上的一点,连接PO,PC,过点P作y轴的垂线,垂足为D.
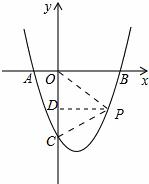
若∠POC=∠PCO,则PD应是线段OC的垂直平分线,∵C的坐标为(0,-3),
∴D的坐标为(0,-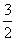 ),∴P的纵坐标应是-
),∴P的纵坐标应是-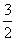 ,令x2-2x-3=-
,令x2-2x-3=-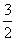 ,解得,x1=
,解得,x1=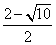 ,x2=
,x2= ,因此所求点P的坐标是(
,因此所求点P的坐标是(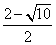 ,-
,-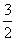 ),(
),( ,-
,-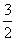 ).
).

练习册系列答案
相关题目
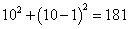 个.
个. .则x-y的值等于( )
.则x-y的值等于( )
 的解在数轴上表示为( )
的解在数轴上表示为( )

 的图象位于第一、第三象限,则k的取值范围是
的图象位于第一、第三象限,则k的取值范围是 的图象交于A、B两点.
的图象交于A、B两点.
 果
果 ,根据图象直接写出
,根据图象直接写出 的取值范围
的取值范围 的值为( )
的值为( )
 B.3 C.
B.3 C.
 D.2
D.2