题目内容
 如图,两个反比例函数
如图,两个反比例函数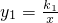 (其中k1>0)和
(其中k1>0)和 在第一象限内的图象依次是C1和C2,点P在C1上.矩形PCOD交C2于A、B两点,OA的延长线交C1于点E,EF垂直x轴于F点,且图中阴影部分面积为13,则EF:AC为
在第一象限内的图象依次是C1和C2,点P在C1上.矩形PCOD交C2于A、B两点,OA的延长线交C1于点E,EF垂直x轴于F点,且图中阴影部分面积为13,则EF:AC为
- A.2﹕1
- B.3﹕1
- C.4﹕

- D.2﹕

C
分析:首先根据反比例函数y2= 的解析式可得到S△ODB=S△OAC=
的解析式可得到S△ODB=S△OAC= ×3=
×3= ,再知阴影部分面积为13可得到S矩形PDOC=16,从而得到图象C1的函数关系式为y=
,再知阴影部分面积为13可得到S矩形PDOC=16,从而得到图象C1的函数关系式为y=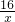 ,再算出△EOF的面积,可以得到△AOC与△EOF的面积比,然后证明△EOF∽△AOC,根据对应边之比等于面积比的平方可得到EF﹕AC的值.
,再算出△EOF的面积,可以得到△AOC与△EOF的面积比,然后证明△EOF∽△AOC,根据对应边之比等于面积比的平方可得到EF﹕AC的值.
解答:∵B、C反比例函数y2= 的图象上,
的图象上,
∴S△ODB=S△OAC= ×3=
×3= ,
,
∵P在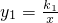 的图象上,
的图象上,
∴S矩形PDOC=k1=13+ +
+ =16,
=16,
∴图象C1的函数关系式为y=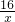 ,
,
∵E点在图象C1上,
∴S△EOF= ×16=8,
×16=8,
∴ =
= =
= ,
,
∵AC⊥x轴,EF⊥x轴,
∴AC∥EF,
∴△EOF∽△AOC,
∴ =
=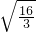 =4:
=4: ,
,
故选:C.
点评:此题主要考查了反比例函数系数k的几何意义,以及相似三角形的性质,关键是掌握在反比例函数y= 图象中任取一点,过这一个点向x轴和y轴分别作垂线,与坐标轴围成的矩形的面积是定值|k|;在反比例函数的图象上任意一点象坐标轴作垂线,这一点和垂足以及坐标原点所构成的三角形的面积是
图象中任取一点,过这一个点向x轴和y轴分别作垂线,与坐标轴围成的矩形的面积是定值|k|;在反比例函数的图象上任意一点象坐标轴作垂线,这一点和垂足以及坐标原点所构成的三角形的面积是 |k|,且保持不变.
|k|,且保持不变.
分析:首先根据反比例函数y2=
 的解析式可得到S△ODB=S△OAC=
的解析式可得到S△ODB=S△OAC= ×3=
×3= ,再知阴影部分面积为13可得到S矩形PDOC=16,从而得到图象C1的函数关系式为y=
,再知阴影部分面积为13可得到S矩形PDOC=16,从而得到图象C1的函数关系式为y=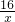 ,再算出△EOF的面积,可以得到△AOC与△EOF的面积比,然后证明△EOF∽△AOC,根据对应边之比等于面积比的平方可得到EF﹕AC的值.
,再算出△EOF的面积,可以得到△AOC与△EOF的面积比,然后证明△EOF∽△AOC,根据对应边之比等于面积比的平方可得到EF﹕AC的值.解答:∵B、C反比例函数y2=
 的图象上,
的图象上,∴S△ODB=S△OAC=
 ×3=
×3= ,
,∵P在
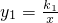 的图象上,
的图象上,∴S矩形PDOC=k1=13+
 +
+ =16,
=16,∴图象C1的函数关系式为y=
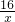 ,
,∵E点在图象C1上,
∴S△EOF=
 ×16=8,
×16=8,∴
 =
= =
= ,
,∵AC⊥x轴,EF⊥x轴,
∴AC∥EF,
∴△EOF∽△AOC,
∴
 =
=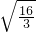 =4:
=4: ,
,故选:C.
点评:此题主要考查了反比例函数系数k的几何意义,以及相似三角形的性质,关键是掌握在反比例函数y=
 图象中任取一点,过这一个点向x轴和y轴分别作垂线,与坐标轴围成的矩形的面积是定值|k|;在反比例函数的图象上任意一点象坐标轴作垂线,这一点和垂足以及坐标原点所构成的三角形的面积是
图象中任取一点,过这一个点向x轴和y轴分别作垂线,与坐标轴围成的矩形的面积是定值|k|;在反比例函数的图象上任意一点象坐标轴作垂线,这一点和垂足以及坐标原点所构成的三角形的面积是 |k|,且保持不变.
|k|,且保持不变. 
练习册系列答案
相关题目
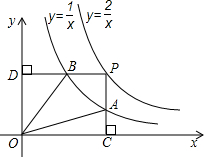 如图,两个反比例函数y=
如图,两个反比例函数y=| 2 |
| x |
| 1 |
| x |
| 2 |
| x |
| 1 |
| x |
| 1 |
| x |
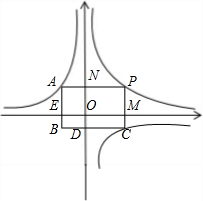 如图,两个反比例函数y=
如图,两个反比例函数y=| k1 |
| x |
| k2 |
| x |
| A、|k1-k2| | ||
B、
| ||
| C、|k1•k2| | ||
D、
|
 (2012•德州)如图,两个反比例函数
(2012•德州)如图,两个反比例函数 如图,两个反比例函数y=
如图,两个反比例函数y=