题目内容
13.对于抛物线y=ax2+bx+c(a≠0),有下列说法:①当b=a+c时,则抛物线y=ax2+bx+c一定经过一个定点(-1,0);
②若△=b2-4ac>0,则抛物线y=cx2+bx+a与x轴必有两个不同的交点;
③若b=2a+3c,则抛物线y=ax2+bx+c与x轴必有两个不同的交点;
④若a>0,b>a+c,则抛物线y=ax2+bx+c与x轴必有两个不同的交点;
其中正确的有①②③④.
分析 利用二次函数的性质以及抛物线与x轴的交点坐标逐一分析得出答案即可.
解答 解:①抛物线y=ax2+bx+c一定经过一个定点(-1,0),则0=a-b+c,即b=a+c,此选项成立成立;
②因为抛物线y=cx2+bx+a,c≠0,△>0,所以抛物线y=cx2+bx+a与x轴必有两个不同的交点,此选项成立成立;
③当b=2a+3c,则b2-4ac=(2a+3b)2-4ac=4a2+8ac+9b2=4(a+c)2+5c2,而a≠0,于是b2-4ac>0,则方程必有两个不相等的实数根;
④当a>0,b>a+c,
若c≥0,则b2-4ac>(a+c)2-4ac=(a-c)2≥0,此时抛物线y=ax2+bx+c与x轴两个不同的交点;
若c<0,则-2ac>0,b2-4ac>0,抛物线y=ax2+bx+c与x轴两个不同的交点
综上,抛物线y=ax2+bx+c与x轴必有两个不同的交点,结论成立.
正确的结论是①②③④.
故答案为:①②③④.
点评 此题考查抛物线与x轴的交点坐标,二次函数的性质,掌握二次函数与一元二次方程的关系,一元二次方程根与系数的关系及二次函数的性质是解决问题的关键.

练习册系列答案
 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目
1.用一个平面去截一个几何体,得到的截面是八边形,这个几何体可能是( )
| A. | 四棱柱 | B. | 五棱柱 | C. | 六棱锥 | D. | 七棱柱 |
5.“十•一”黄金周期间,威海华夏城在7天假期中每天接待游客的人数变化如下表(正数表示比前一天多的人数,负数表示比前一天少的人数)
(1)若9月30日的游客人数为1.2千人,则10月2日的游客人数为2.6千人;
(2)七天内游客人数最多的一天是10月4日,人数达到2.8千人.
(3)若门票每人80元,请求出黄金周期间威海华夏城门票总收入是多少万元?
| 日期 | 1日 | 2日 | 3日 | 4日 | 5日 | 6日 | 7日 |
| 人数变化(千人) | +0.6 | +0.8 | -0.4 | +0.6 | -0.8 | +0.2 | -1.4 |
(2)七天内游客人数最多的一天是10月4日,人数达到2.8千人.
(3)若门票每人80元,请求出黄金周期间威海华夏城门票总收入是多少万元?
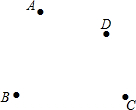 如图,平面上有A,B,C,D四个点,按照下列要求画图:
如图,平面上有A,B,C,D四个点,按照下列要求画图: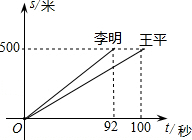 读图填空:如图这是李明、王平两人在一次赛跑中,路程s与时间t的关系,
读图填空:如图这是李明、王平两人在一次赛跑中,路程s与时间t的关系,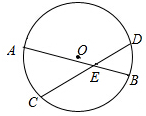 如图,AB,CD是⊙O的两条弦,交于点E,$\widehat{AC}$=80°,$\widehat{BD}$=60°,则∠BED=70°.
如图,AB,CD是⊙O的两条弦,交于点E,$\widehat{AC}$=80°,$\widehat{BD}$=60°,则∠BED=70°. ⊙O为△ABC的内切圆,⊙O与AB相切于D,△ABC周长为12,BC=4,则AD=2.
⊙O为△ABC的内切圆,⊙O与AB相切于D,△ABC周长为12,BC=4,则AD=2.