题目内容
3. ⊙O为△ABC的内切圆,⊙O与AB相切于D,△ABC周长为12,BC=4,则AD=2.
⊙O为△ABC的内切圆,⊙O与AB相切于D,△ABC周长为12,BC=4,则AD=2.
分析 由切线长定理得出AD=AE,BD=BF,CE=CF,设AE=AD=x,CF=CE=y,则BD=BF=4-y,根据题意得出方程,解方程求出x即可.
解答 解:根据切线长定理得:AD=AE,BD=BF,CE=CF,
设AE=AD=x,CF=CE=y,
则BD=BF=4-y,
根据题意得:x+4-y+4-y+y+y+x=12,
解得:x=2,
即AD=2.
故答案为:2.
点评 本题考查了三角形的内切圆与内心、切线长定理;熟练掌握切线长定理,通过设出未知数得出方程是解决问题的关键.

练习册系列答案
 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案
相关题目
15.一个三角形的两边长为4和6,第三边的边长是方程(x-2)(x-7)=0的两根,则这个三角形的周长是( )
| A. | 12 | B. | 12或17 | C. | 17 | D. | 19 |
12.a为有理数,下列说法中正确的是( )
| A. | -a一定是负数 | B. | -a2一定是负数 | C. | (-a)3一定是负数 | D. | |a|一定不是负数 |
13.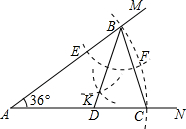 如图,小明作图如下:
如图,小明作图如下:
(1)用量角器作∠MAN=36°;
(2)以A为圆心适当长为半径作圆弧,分别交AM,AN于B,C两点,连结BC;
(3)以B为圆心适当长为半径作圆弧,分别交AB,BC于E,F两点,再分别以E,F为圆心大于$\frac{1}{2}$EF长为半径作圆弧,两条圆弧交于点K,连结BK并延长交AC于点D.
若AD=a,则由以上作图可得AB为( )
 如图,小明作图如下:
如图,小明作图如下:(1)用量角器作∠MAN=36°;
(2)以A为圆心适当长为半径作圆弧,分别交AM,AN于B,C两点,连结BC;
(3)以B为圆心适当长为半径作圆弧,分别交AB,BC于E,F两点,再分别以E,F为圆心大于$\frac{1}{2}$EF长为半径作圆弧,两条圆弧交于点K,连结BK并延长交AC于点D.
若AD=a,则由以上作图可得AB为( )
| A. | $\frac{\sqrt{5}-1}{2}$a | B. | $\frac{3-\sqrt{5}}{2}$a | C. | $\frac{\sqrt{5}+1}{2}a$ | D. | $\frac{3+\sqrt{5}}{2}$a |
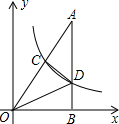 如图,Rt△AOB的一条直角边OB在x轴上,双曲线y=$\frac{k}{x}$(x>0)经过斜边OA的中点C,与另一直角边交于点D,若S△OCD=3,则k的值为4.
如图,Rt△AOB的一条直角边OB在x轴上,双曲线y=$\frac{k}{x}$(x>0)经过斜边OA的中点C,与另一直角边交于点D,若S△OCD=3,则k的值为4.