Question

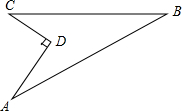如图所示的一块地，已知AD=4米，CD=3米，∠ADC=90°，AB=13米，BC=12米，这块地的面积为

 

．

Answer 1

分析：连接AC，利用勾股定理可以得出三角形ACD和ABC是直角三角形，△ABC的面积减去△ACD的面积就是所求的面积．

解答：解：如图，连接AC
由勾股定理可知
AC=

AD2+CD 2

=

42+32

=5，
又AC²+BC²=5²+12²=13²=AB²
故三角形ABC是直角三角形
故所求面积=△ABC的面积-△ACD的面积=

1

2

×5×12-

1

2

×3×4=24（m²）．

点评：考查了直角三角形面积公式以及勾股定理的应用．