Question

如图，所示的两条抛物线的解析式分别是y₁=-mx²-mx+1，y₂=mx²-mx-1（其中m为常数，且m＞0）．请写出三条与上述抛物线有关的不同类型的结论：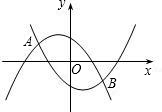

 

Answer 1

分析：据图象和两条抛物线的解析式y₁=-mx²-mx+1，y₂=mx²-mx-1（其中m为常数，且m＞0），可得：①开口方向不同；②顶点坐标不同；③与x轴的交点不同④对称轴不同⑤与y轴的交点不同；⑥出两个交点外，图象经过的其它的点不同．

解答：解：①抛物线y₁=-mx²-mx+1开口向下，抛物线y₂=mx²-mx-1开口向上；
②抛物线y₁=-mx²-mx+1的对称轴是x=-

1

2

，抛物线y₂=mx²-mx-1的对称轴是x=

1

2

；
③抛物线y₁=-mx²-mx+1经过点（0，1），抛物线y₂=mx²-mx-1经过点（0，-1）；

点评：本题考查对二次函数解析式和图象的理解掌握情况．