题目内容
10.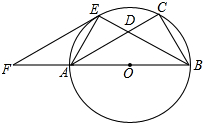 如图,已知以Rt△ABC的斜边AB为直径作△ABC的外接圆⊙O,∠ABC的平分线BE交AC于D,交⊙O于E,过E作EF∥AC交BA的延长线于F.
如图,已知以Rt△ABC的斜边AB为直径作△ABC的外接圆⊙O,∠ABC的平分线BE交AC于D,交⊙O于E,过E作EF∥AC交BA的延长线于F.(1)求证:EF是⊙O切线;
(2)若EF=8,tan∠AEF=$\frac{1}{2}$,求CD的长.
分析 (1)连结OE,交AC于G点,如图,由∠ABE=∠CBE得$\widehat{AE}$=$\widehat{CE}$,则根据垂径定理得到OE⊥AC,而EF∥AC,根据平行线的性质得OE⊥EF,于是根据切线的判定定理得到EF是⊙O切线;
(2)根据平行线的性质由AG∥EF得∠EAG=∠AEF,在Rt△AEG中,利用正切的定义得tan∠EAG=$\frac{EG}{AG}$=$\frac{1}{2}$,设EG=x,⊙O的半径为r,则AG=2x,OG=r-x,在Rt△AGO中,利用勾股定理可得r=$\frac{5}{2}$x,则OG=$\frac{3}{2}$x,在证明△OAG∽△OFE,利用相似比可计算出AG=$\frac{24}{5}$,所以x=$\frac{12}{5}$,则OG=$\frac{18}{5}$,接着利用三角形中位线性质得BC=2OG=$\frac{36}{5}$,然后根据圆周角定理得∠CBD=∠EAC,于是在Rt△BCD中,利用tan∠CBD=$\frac{CD}{BC}$=$\frac{1}{2}$可计算出CD.
解答 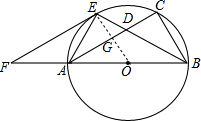 (1)证明:连结OE,交AC于G点,如图,
(1)证明:连结OE,交AC于G点,如图,
∵BE平分∠ABC,
∴∠ABE=∠CBE,
∴$\widehat{AE}$=$\widehat{CE}$,
∴OE⊥AC,
∵EF∥AC,
∴OE⊥EF,
∴EF是⊙O切线;
(2)解:∵AG∥EF,
∴∠EAG=∠AEF,
在Rt△AEG中,tan∠EAG=$\frac{EG}{AG}$=$\frac{1}{2}$,
设EG=x,⊙O的半径为r,则AG=2x,OG=r-x,
在Rt△AGO中,(2x)2+(r-x)2=r2,则r=$\frac{5}{2}$x,
∴OG=$\frac{3}{2}$x,
∵AG∥EF,
∴△OAG∽△OFE,
∴$\frac{AG}{EF}$=$\frac{OG}{OE}$,即$\frac{AG}{8}$=$\frac{\frac{3}{2}r}{\frac{5}{2}r}$,则AG=$\frac{24}{5}$,
∴x=$\frac{12}{5}$,
∴OG=$\frac{18}{5}$,
∵OA=OB,AG=CG,
∴OG=$\frac{1}{2}$BC,
∴BC=2OG=$\frac{36}{5}$,
∵∠CBD=∠EAC,
∴tan∠CBD=$\frac{1}{2}$,
在Rt△BCD中,∵tan∠CBD=$\frac{CD}{BC}$=$\frac{1}{2}$,
∴CD=$\frac{1}{2}$BC=$\frac{18}{5}$.
点评 本题考查了切线的判定:经过半径的外端且垂直于这条半径的直线是圆的切线.要证某线是圆的切线,已知此线过圆上某点,连接圆心与这点(即为半径),再证垂直即可.也考查了圆周角定理、垂径定理和相似三角形的判定与性质.

 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案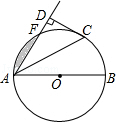 如图,AB是⊙O的直径,点F,C是⊙O上两点,且$\widehat{AF}$=$\widehat{FC}$=$\widehat{CB}$,连接AC,AF,过点C作CD⊥AF交AF延长线于点D,垂足为D.
如图,AB是⊙O的直径,点F,C是⊙O上两点,且$\widehat{AF}$=$\widehat{FC}$=$\widehat{CB}$,连接AC,AF,过点C作CD⊥AF交AF延长线于点D,垂足为D.
 如图所示,E是平行四边形ABCD内任意一点,若平行四边形的面积是S,则图中阴影部分的面积是多少?
如图所示,E是平行四边形ABCD内任意一点,若平行四边形的面积是S,则图中阴影部分的面积是多少? 如图,⊙O的直径AB=4,弦DE垂直平分半径OA,点C为垂足
如图,⊙O的直径AB=4,弦DE垂直平分半径OA,点C为垂足