题目内容
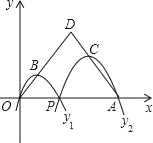
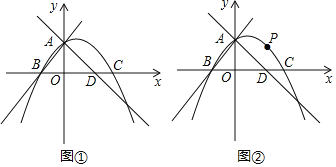
【题目】如图①,抛物线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,将直线
,将直线![]() 绕点
绕点![]() 逆时针旋转90°,所得直线与
逆时针旋转90°,所得直线与![]() 轴交于点
轴交于点![]() .
.
(1)求直线![]() 的函数解析式;
的函数解析式;
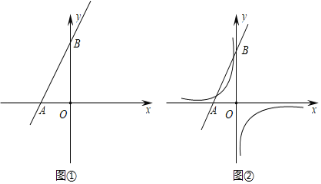
(2)如图②,若点![]() 是直线
是直线![]() 上方抛物线上的一个动点
上方抛物线上的一个动点
①当点![]() 到直线
到直线![]() 的距离最大时,求点
的距离最大时,求点![]() 的坐标和最大距离;
的坐标和最大距离;
②当点![]() 到直线
到直线![]() 的距离为
的距离为![]() 时,求
时,求![]() 的值.
的值.
【答案】(1)![]() ;(2)①当点
;(2)①当点![]() 到直线
到直线![]() 的距离最大时,点
的距离最大时,点![]() 的坐标是
的坐标是![]() ,最大距离是
,最大距离是![]() ;②
;②![]() 的值是
的值是![]() 或
或![]() .
.
【解析】
(1)根据已知条件可计算出点A、B、C的坐标,再证明OA=OD,即可得D点的坐标,因此可得AD所在直线的解析式.
(2)①作![]() 轴交直线
轴交直线![]() 于点
于点![]() ,设P点的横坐标为t,因为P在抛物线上因此可得纵坐标为
,设P点的横坐标为t,因为P在抛物线上因此可得纵坐标为![]() ,因为N点在直线AD上因此可得N
,因为N点在直线AD上因此可得N![]() ,根据三角函数可得PH的长度,再利用二次函数可得PH取最大值时t的值,进而计算出P点的坐标; ② 解二元一次方程即可得到t的值,再根据t的值计算
,根据三角函数可得PH的长度,再利用二次函数可得PH取最大值时t的值,进而计算出P点的坐标; ② 解二元一次方程即可得到t的值,再根据t的值计算![]() 即可.
即可.
解:(1)当![]() 时
时![]() ,则点
,则点![]() 的坐标为
的坐标为![]() ,
,
当![]() 时,
时,![]() ,解得,
,解得,![]() ,则点
,则点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵将直线![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 得到直线
得到直线![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴点![]() 的坐标为
的坐标为![]() ,
,
设直线![]() 的函数解析式为
的函数解析式为![]()
![]() ,得
,得![]() ,
,
即直线![]() 的函数解析式为
的函数解析式为![]() ;
;
(2)作![]() 轴交直线
轴交直线![]() 于点
于点![]() ,如图①所示,
,如图①所示,
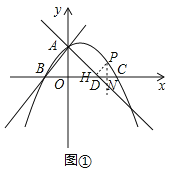
设点![]() 的坐标为
的坐标为![]() ,则点
,则点![]() 的坐标为
的坐标为![]() ,
,
∴![]() ,
,
∴![]() 轴,
轴,
∴![]() 轴,
轴,
∴![]() ,
,
作![]() 于点
于点![]() ,则
,则![]() ,
,
∴![]() ,
,
∴当![]() 时,
时,![]() 取得最大值
取得最大值![]() ,此时点P的坐标为
,此时点P的坐标为![]() ,
,
即当点![]() 到直线
到直线![]() 的距离最大时,点
的距离最大时,点![]() 的坐标是
的坐标是![]() ,最大距离是
,最大距离是![]() ;
;
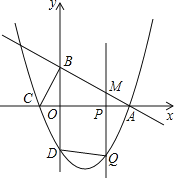
②当点![]() 到直线
到直线![]() 的距离为
的距离为![]() 时,如图②所示,
时,如图②所示,
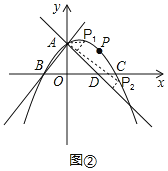
则![]() ,
,
解得:![]() ,
,
则![]() 的坐标为
的坐标为![]() ,
,![]() 的坐标为
的坐标为![]() ,
,
当![]() 的坐标为
的坐标为![]() ,则
,则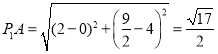 ,
,
∴ ;
;
当![]() 的坐标为
的坐标为![]() ,则
,则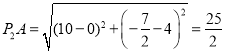 ,
,
∴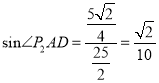 ;
;
由上可得,![]() 的值是
的值是![]() 或
或![]() .
.

练习册系列答案
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案
相关题目