Question

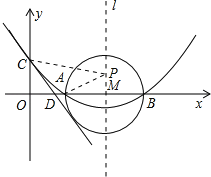
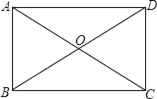
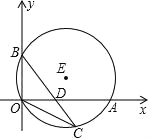
【题目】如图，直径为13的⊙E，经过原点O，并且与x轴、y轴分别交于A、B两点，线段OA、OB(OA＞OB)的长分别是方程x2+kx+60＝0的两根．

(1)OA：OB＝____；

(2)若点C在劣弧OA上，连结BC交OA于D，当△BOC∽△BDA时，点D的坐标为______．

Answer 1

【答案】（1）12：5；（2）（，0）．

【解析】

试题解析：连接AB，

∵∠AOB=90°，

∴AB是⊙E的直径，AB=13，

∴OA2+OB2=AB2=169．

根据根与系数的关系可得：

OA+OB=-k＞0，OA×OB=60，

∴OA2+OB2=（OA+OB）2-2OAOB=k2-120=169，

∴k=-17，

原方程为x2-17x+60=0，

解得x1=5，x2=12，

∴OA=12，OB=5，

∴OA：OB=12：5．

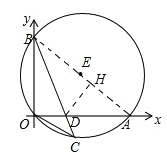
（2）过点D作DH⊥AB于H，如图．

∵△BOC∽△BDA，

∴∠OBC=∠DBA，

在△BOD和△BHD中，

，

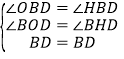∴△BOD≌△BHD，

∴BH=BO=5，DH=OD．

设OD=x，则DH=x，DA=12-x．

在Rt△DHA中，根据勾股定理可得，

x2+（13-5）2=（12-x）2，

解得x=，

∴点D的坐标为（，0）．