题目内容
15.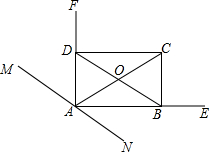 如图,直线MN经过线段AC的端点,过点A作直线MN∥BD,点B,D分别在∠NAC和∠MAC的角平分线AE,AF上,BD交AC于点O.
如图,直线MN经过线段AC的端点,过点A作直线MN∥BD,点B,D分别在∠NAC和∠MAC的角平分线AE,AF上,BD交AC于点O.(1)求证:OB=OD;
(2)若AD=5,AB=12,求OA的长;
(3)当点O在边AC上运动到什么位置时,四边形ABCD是矩形?并说明理由.
分析 (1)首先根据角平分线的性质得到∠CAE=∠NAE,然后根据MN∥BD得到∠OBA=∠NAB,从而得到∠OAB=∠OBA,利用等边对等角得到OA=OB,同理可得:OA=OD,进而证得结论:OB=OD;
(2)首先得到∠DAB=90°,然后利用勾股定理求得BD的长,从而利用直角三角形的斜边的中线等于斜边的一半求得结论;
(3)由一对邻补角的平分线互相垂直得出∠FAE=90°,要想四边形ABCD是矩形,只需证明四边形ABCD是平行四边形.
解答 解:(1)证明:∵AE平分∠CAN,
∴∠CAE=∠NAE,
∵MN∥BD,
∴∠OBA=∠NAB,
∴∠OAB=∠OBA,
∴OA=OB,
同理可得:OA=OD,
∴OB=OD;
(2)∵∠CAE=∠NAE,∠MAD=∠OAD,
∴∠DAB=∠BAO+∠DAO=$\frac{1}{2}$×180°=90°,
∵AD=5,AB=12,
∴BD=13,
∴OA=$\frac{1}{2}$BD=$\frac{13}{2}$;
(3)O在AC的中点时,四边形ABCD是矩形.
∵AO=CO,BO=DO,
∴四边形ABCD是平行四边形,
又∵∠FAC=$\frac{1}{2}$∠MAC,∠CAE=$\frac{1}{2}$∠CAN,
∴∠FAE=∠FAC+∠CAE=$\frac{1}{2}$(∠MAC+∠CAN)=$\frac{1}{2}$×180°=90°,
∴平行四边形ABCD是矩形.
点评 本题考查矩形的判定及勾股定理的知识,解题的关键是了解:有一个角是直角的平行四边形是矩形,难度不大.

练习册系列答案
相关题目
3.我市5月的某一周每天的最高气温(单位:℃)统计如下:29,20,27,22,24,26,27,则这组数据的中位数与众数分别是( )
| A. | 24,27 | B. | 26,27 | C. | 26,24 | D. | 20,24 |
20.计算:$\frac{{{{(-ab)}^2}}}{{{a^2}b}}$的结果是( )
| A. | a | B. | b | C. | -b | D. | 1 |
7.下列图形中不是中心对称图形,而是轴对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
4.下列多项式中不能用公式进行因式分解的是( )
| A. | a2+a+$\frac{1}{4}$ | B. | a2+b2-2ab | C. | -a2+25b2 | D. | -4-b2 |