题目内容
17.A4纸是由国际标准化组织的ISO216定义的,世界上多数国家所使用的纸张尺寸都是采用这一国际标准.将一张A4纸沿着长边中点对折后,得到的矩形与原矩形相似,则A4纸长与宽的比值是$\sqrt{2}$:1.分析 矩形ABCD对折后所得矩形与原矩形相似,则矩形ABCD∽矩形BFEA,设矩形的长为a,宽为b.则AB=CD=b,AD=BC=a,BF=AE=$\frac{a}{2}$,根据矩形相似,对应边的比相等得到比例式,计算即可.
解答 解:设矩形的长为a,宽为b,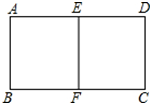
则AB=CD=b,AD=BC=a,BF=AE=$\frac{a}{2}$,
∵矩形ABCD∽矩形BFEA,
∴$\frac{AE}{AB}$=$\frac{AB}{AD}$,
即$\frac{\frac{a}{2}}{b}$=$\frac{b}{a}$,
∴a:b=$\sqrt{2}$:1.
故答案为:$\sqrt{2}$:1.
点评 本题考查的是相似多边形的性质,掌握相似多边形的对应边的比相等是解题的关键.

练习册系列答案
相关题目
5.一个两位数,个位数字为a,十为数字为b,则这个两位数为( )
| A. | ab | B. | ba | C. | 10a+b | D. | 10b+a |
6.下列从左到右的变形,是分解因式的是( )
| A. | xy2(x-1)=x2y2-xy2 | B. | x2+x-5=(x-2)(x+3)+1 | C. | (a+3)(a-3)=a2-9 | D. | 2a2+4a=2a(a+2) |
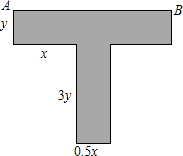 某种T型零件尺寸如图所示(左右宽度相同),求:
某种T型零件尺寸如图所示(左右宽度相同),求: 所给的数轴上表示下列四个数,并把这四个数按从小到大的顺序,用“<”号连接起来.
所给的数轴上表示下列四个数,并把这四个数按从小到大的顺序,用“<”号连接起来.