题目内容
3.已知平面直角坐标系xOy,抛物线y=-x2+bx+c过点A(4,0)、B(1,3).(1)求该抛物线的表达式,并写出该抛物线的对称轴和顶点坐标;
(2)记该抛物线的对称轴为直线l,设抛物线上的点P(5,n)关于直线l的对称点为E,求四边形AOEP的面积.
分析 (1)用待定系数法求出抛物线的解析式,运用配方法求出对称轴和顶点坐标;
(2)根据点P(5,n)在抛物线上,求出点P的坐标,根据抛物线的对称性求出PE的长,根据梯形面积的求法求出四边形AOEP的面积.
解答 解:(1)由题意得,
$\left\{\begin{array}{l}{-16+4b+c=0}\\{-1+b+c=3}\end{array}\right.$,
解得$\left\{\begin{array}{l}{b=4}\\{c=0}\end{array}\right.$,
∴该抛物线的表达式为:y=-x2+4x,
∵y=-x2+4x=-(x-2)2+4,
∴抛物线的对称轴是x=2,和顶点坐标(2,4);
(2)当x=5时,y=-5,∴点P(5,-5),
∵点P(5,-5)与点E关于x=2对称,∴PE=6,
又∵OA=4,
∴四边形AOEP的面积为:$\frac{1}{2}$(4+6)×5=25.
点评 本题考查的是待定系数法求二次函数的解析式和二次函数的性质,正确运用待定系数法是解题的关键,注意正确运用配方法求抛物线的对称轴和顶点坐标.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
11.有4万个不小于70的两位数,从中随机抽取了3000个数据,统计如下:
请根据表格中的信息,估计这4万个数据的平均数约为( )
| 数据x | 70<x<79 | 80<x<89 | 90<x<99 |
| 个数 | 800 | 1300 | 900 |
| 平均数 | 78.1 | 85 | 91.9 |
| A. | 92.16 | B. | 85.23 | C. | 84.73 | D. | 77.97 |
18.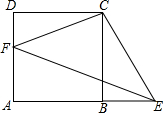 如图,正方形ABCD中,点F在AD上,点E在AB的延长线上,∠FCE=90°
如图,正方形ABCD中,点F在AD上,点E在AB的延长线上,∠FCE=90°
(1)求证:△CDF≌△CBE;
(2)如果正方形ABCD的面积为64,Rt△CEF的面积为50,则线段BE的长为多少?
 如图,正方形ABCD中,点F在AD上,点E在AB的延长线上,∠FCE=90°
如图,正方形ABCD中,点F在AD上,点E在AB的延长线上,∠FCE=90°(1)求证:△CDF≌△CBE;
(2)如果正方形ABCD的面积为64,Rt△CEF的面积为50,则线段BE的长为多少?
15.下列运算正确的是( )
| A. | a2+a3=a5 | B. | a3×a2=a6 | C. | (a3)3=a6 | D. | a8÷a2=a6 |
12.下列计算正确的是( )
| A. | -$\sqrt{(-8)^{2}}$=-8 | B. | (-$\sqrt{8}$)2=64 | C. | $\sqrt{(-25)^{2}}$=±25 | D. | $\sqrt{9\frac{1}{16}}$=3$\frac{1}{4}$ |
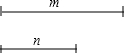 如图,已知线段m、n,利用直尺和圆规作图(不写作法,保留作图痕迹)作Rt△ABC,使∠ACB=90°,AB=m,BC=n.
如图,已知线段m、n,利用直尺和圆规作图(不写作法,保留作图痕迹)作Rt△ABC,使∠ACB=90°,AB=m,BC=n.