题目内容
3.选择适当的方法解以下方程;(1)3x(x-1)=x(x+5)
(2)(x-3)(x+2)=6
(3)4(x+3)2=25(x-2)2.
分析 (1)先移项得到3x(x-1)-x(x+5)=0,然后利用因式分解法解方程;
(2)先把方程化为一般式,然后利用因式分解法解方程;
(3)先移项得到4(x+3)2-25(x-2)2=0,然后利用因式分解法解方程.
解答 解:(1)3x(x-1)-x(x+5)=0,
x(3x-3-x-5)=0,
x=0或3x-3-x-5=0,
所以x1=0,x2=4;
(2)x2-x-12=0,
(x-4)(x+3)=0,
x-4=0或x+3=0,
所以x1=4,x2=-3;
(3)4(x+3)2-25(x-2)2=0,
[2(x+3)+5(x-2)][2(x+3)-5(x-2)]=0,
2(x+3)+5(x-2)=0或2(x+3)-5(x-2)=0,
所以x1=$\frac{4}{7}$,x2=$\frac{16}{3}$.
点评 本题考查了解一元二次方程-因式分解法:先把方程的右边化为0,再把左边通过因式分解化为两个一次因式的积的形式,那么这两个因式的值就都有可能为0,这就能得到两个一元一次方程的解,这样也就把原方程进行了降次,把解一元二次方程转化为解一元一次方程的问题了(数学转化思想).

练习册系列答案
相关题目
2.根据下列条件,得不到平行四边形的是( )
| A. | AB=CD,AD=BC | B. | AB∥CD,AB=CD | C. | AB=CD,AD∥BC | D. | AB∥CD,AD∥BC |
19. 如图,C是⊙O上一点,O是圆心,若∠C=35°,则∠AOB的度数为( )
如图,C是⊙O上一点,O是圆心,若∠C=35°,则∠AOB的度数为( )
 如图,C是⊙O上一点,O是圆心,若∠C=35°,则∠AOB的度数为( )
如图,C是⊙O上一点,O是圆心,若∠C=35°,则∠AOB的度数为( )| A. | 35° | B. | 55° | C. | 70° | D. | 105° |
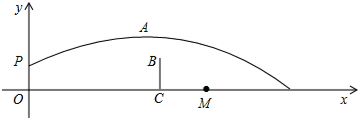
 如图,在△ABC中,∠ACB=90°,AB上一点O在BC的垂直平分线上.探究点O是否在AC的垂直分线上?
如图,在△ABC中,∠ACB=90°,AB上一点O在BC的垂直平分线上.探究点O是否在AC的垂直分线上?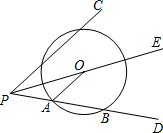 如图,射线PE平分∠CPD,O为射线PE上一点,以O为圆心作⊙O,与PD边交于点A、点B,连结OA,且OA∥PC.
如图,射线PE平分∠CPD,O为射线PE上一点,以O为圆心作⊙O,与PD边交于点A、点B,连结OA,且OA∥PC.