题目内容
20.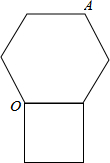 如图,正方形和正六边形的边长都为1,如图所示摆放,正六边形按顺时针方向,在正方形边上旋转一周,假设A旋转一周后到达A′的位置,连接OA,OA′,则OA,OA′,与A所经过路线所围成的封闭图形面积为$\frac{5π}{3}$.
如图,正方形和正六边形的边长都为1,如图所示摆放,正六边形按顺时针方向,在正方形边上旋转一周,假设A旋转一周后到达A′的位置,连接OA,OA′,则OA,OA′,与A所经过路线所围成的封闭图形面积为$\frac{5π}{3}$.
分析 根据题意画出图形,可知A旋转一周后,所形成的封闭图形的面积为S扇形ABA1+S扇形A1CA2,计算出扇形面积,相加即可.
解答  解:如图,A旋转一周后,所形成的封闭图形的面积为S扇形ABA1+S扇形A1CA2.
解:如图,A旋转一周后,所形成的封闭图形的面积为S扇形ABA1+S扇形A1CA2.
∵AB=$\sqrt{3}$OB=$\sqrt{3}$,∠ABA1=360°-210°=150°,
∴S扇形ABA1=$\frac{150π(\sqrt{3})^{2}}{360}$=$\frac{5π}{4}$;
∵CA2=1,∠A2CA1=360°-210°=150°,
∴S扇形A1CA2=$\frac{150π×{1}^{2}}{360}$=$\frac{5}{12}$π;
∴S扇形ABA1+S扇形A1CA2=$\frac{5π}{4}$+$\frac{5π}{12}$=$\frac{5π}{3}$.
故答案为$\frac{5π}{3}$.
点评 本题考查了扇形的面积和轨迹,正确作出A的轨迹并正确应用扇形面积公式是解题的关键.

练习册系列答案
相关题目
12.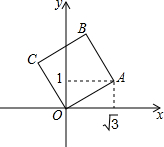 如图,将正方形OABC放在平面直角坐标系中,O是原点,A的坐标为($\sqrt{3}$,1),则点C的坐标为( )
如图,将正方形OABC放在平面直角坐标系中,O是原点,A的坐标为($\sqrt{3}$,1),则点C的坐标为( )
 如图,将正方形OABC放在平面直角坐标系中,O是原点,A的坐标为($\sqrt{3}$,1),则点C的坐标为( )
如图,将正方形OABC放在平面直角坐标系中,O是原点,A的坐标为($\sqrt{3}$,1),则点C的坐标为( )| A. | (-$\sqrt{3}$,1) | B. | (-1,-$\sqrt{3}$) | C. | (-1,$\sqrt{3}$) | D. | (1,-$\sqrt{3}$) |
9.某品牌折扣店将某件衣服按进价提高50%后标价,再打八折销售,获利40元.设这件的进价为x元,根据题意,下面所列方程正确的是( )
| A. | x•50%×80%-x=40 | B. | x(1+50%)×80%-x=40 | ||
| C. | (x+50%)•80%-x=40 | D. | x(1+50%)(1-20%)-x=40 |
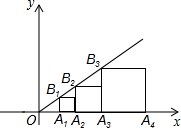 如图,直线y=$\frac{\sqrt{3}}{3}$x,点A1的坐标为(1,0),过点A1作x轴的垂线交直线于点B1,以A1B1为边长,作正方形交x轴于A2,再过点A2作x轴的垂线交直线于点B2,以A2B2为边长作正方形交x轴于点A3,…,按此作法进行下去,则OA3的长为$\frac{4}{3}$+$\frac{2\sqrt{3}}{3}$.
如图,直线y=$\frac{\sqrt{3}}{3}$x,点A1的坐标为(1,0),过点A1作x轴的垂线交直线于点B1,以A1B1为边长,作正方形交x轴于A2,再过点A2作x轴的垂线交直线于点B2,以A2B2为边长作正方形交x轴于点A3,…,按此作法进行下去,则OA3的长为$\frac{4}{3}$+$\frac{2\sqrt{3}}{3}$.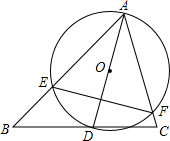 如图,△ABC中,∠BCA=75°,∠ABC=45°,AB=6$\sqrt{2}$,D是线段BC上的一个动点,以AD为直径作⊙O分别交AB、AC于E、F,连接EF,当线段EF长度取最小值时,CD=12-6$\sqrt{3}$.
如图,△ABC中,∠BCA=75°,∠ABC=45°,AB=6$\sqrt{2}$,D是线段BC上的一个动点,以AD为直径作⊙O分别交AB、AC于E、F,连接EF,当线段EF长度取最小值时,CD=12-6$\sqrt{3}$. 如图是一个正方形及其内切圆,随机地往正方形内投一粒米,落在圆内的概率为$\frac{π}{4}$.
如图是一个正方形及其内切圆,随机地往正方形内投一粒米,落在圆内的概率为$\frac{π}{4}$.