题目内容
无论x、y取任何实数，多项式x2+y2-2x-4y+16的值总是 数．
考点：配方法的应用,非负数的性质：偶次方
专题：计算题
分析：多项式配方变形后，利用非负数的性质判断即可．
解答：解：x2+y2-2x-4y+16=（x2-2x+1）+（y2-4y+4）+11=（x-1）2+（y-2）2+11≥11＞0，
当且仅当x=1，y=2时取等号，
则当x=1，y=2时，多项式最小值为11，即多项式的值总是正数．
故答案为：正．
当且仅当x=1，y=2时取等号，
则当x=1，y=2时，多项式最小值为11，即多项式的值总是正数．
故答案为：正．
点评：此题考查了配方法的应用，以及非负数的性质，熟练掌握完全平方公式是解本题的关键．
练习册系列答案
口算题卡加应用题集训系列答案
相关题目
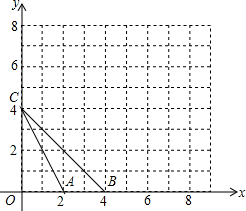如图，在平面直角坐标系中，△ABC的顶点坐标为A（2，0）、B（4，0）、C（0，4），将各顶点的横坐标、纵坐标都乘2，得相应的点A′、B′、C′的坐标．
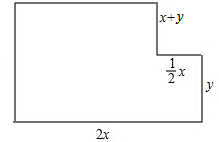为了提高业主的宜居环境，某移民小区规划修建一个休闲场所（平面图形如图所示）．
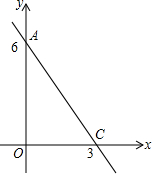已知直线l：y=kx+b经过点A（0，6）且平行于直线y=-2x