题目内容
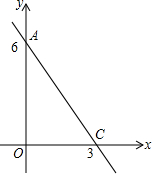 已知直线l:y=kx+b经过点A(0,6)且平行于直线y=-2x
已知直线l:y=kx+b经过点A(0,6)且平行于直线y=-2x(1)直接写出k的值、b的值及直线的解析式;
(2)如果这条直线经过点P(m,2),求m的值;
(3)满足在(2)的条件下,并且直线l与x轴交于点C,在x轴上求一点使S△BPC=2.
考点:两条直线相交或平行问题
专题:计算题
分析:(1)根据一次函数图象上点的坐标特征易得b=6,根据两直线平行的问题易得k=-2,从而可确定直线1的解析式;
(2)根据一次函数图象上点的坐标特征,把(m,2)代入(1)中的解析式即可求出m的值;
(3)先确定C点坐标,设B点坐标为(t,0),然后根据三角形面积公式得到
•2•|t-3|=2,再解绝对值方程求出t的值即可得到B点坐标.
(2)根据一次函数图象上点的坐标特征,把(m,2)代入(1)中的解析式即可求出m的值;
(3)先确定C点坐标,设B点坐标为(t,0),然后根据三角形面积公式得到
| 1 |
| 2 |
解答:解:(1)∵y=kx+b经过点A(0,6),
∴b=6,
∵直线y=kx+b平行于直线y=-2x,
∴k=-2,
∴直线1的解析式为y=-2x+6;
(2)∵直线l经过P(m,2),
∴-2m+6=2,
∴m=2;
(3)当y=0时,-2x+6=0,解得x=3,则C点坐标为(3,0),
设B点坐标为(t,0),
•2•|t-3|=2,
解得t=5或t=1.
所以B点坐标为(1,0)或(5,0).
∴b=6,
∵直线y=kx+b平行于直线y=-2x,
∴k=-2,
∴直线1的解析式为y=-2x+6;
(2)∵直线l经过P(m,2),
∴-2m+6=2,
∴m=2;
(3)当y=0时,-2x+6=0,解得x=3,则C点坐标为(3,0),
设B点坐标为(t,0),
| 1 |
| 2 |
解得t=5或t=1.
所以B点坐标为(1,0)或(5,0).
点评:本题考查了两条直线相交或平行问题:两条直线的交点坐标,就是由这两条直线相对应的一次函数表达式所组成的二元一次方程组的解;若两条直线是平行的关系,那么他们的自变量系数相同,即k值相同.

练习册系列答案
相关题目
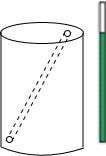 如图所示,一个油漆桶高1m,桶内还有剩余油漆,一根木棒长1.5m,小明把木棒从桶盖小口斜插入桶内,一端触到桶底边缘时,另一端恰好与桶盖小口相齐,抽出木棒,量得木棒上浸沾油漆的部分长0.75m,那么桶内油漆面的高度是多少?(油漆桶水平放置)
如图所示,一个油漆桶高1m,桶内还有剩余油漆,一根木棒长1.5m,小明把木棒从桶盖小口斜插入桶内,一端触到桶底边缘时,另一端恰好与桶盖小口相齐,抽出木棒,量得木棒上浸沾油漆的部分长0.75m,那么桶内油漆面的高度是多少?(油漆桶水平放置)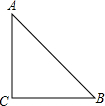 如图,在△ABC中,AC=BC=2cm,∠C=90°,按下列条件建立坐标系,写出顶点的坐标.
如图,在△ABC中,AC=BC=2cm,∠C=90°,按下列条件建立坐标系,写出顶点的坐标.