题目内容
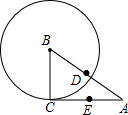 已知在Rt△ABC中,∠C=90°,BC=3cm,AC=4cm,D为AB的中点,E为AC的中点,以B为圆心,BC为半径作⊙B,A、C、D、E与⊙B的位置关系如何?
已知在Rt△ABC中,∠C=90°,BC=3cm,AC=4cm,D为AB的中点,E为AC的中点,以B为圆心,BC为半径作⊙B,A、C、D、E与⊙B的位置关系如何?考点:点与圆的位置关系
专题:
分析:先根据勾股定理求出AB的长,再由点D是AB的中点求出BD的长,进而可得出结论.
解答:解:∵在Rt△ABC中,∠C=90°,BC=3cm,AC=4cm,
∴AB=
=
=5.
∵D为AB的中点,
∴BD=
AB=2.5cm.
∵以B为圆心,BC为半径作⊙B,
∴⊙B的半径为3,点C在圆上.
∵BC⊥AC,
∴直线AC与⊙B相切,C为切点,
∴A,E在圆外.
∵BD<3,
∴点D在圆内.
∴AB=
| BC2+AC2 |
| 32+42 |
∵D为AB的中点,
∴BD=
| 1 |
| 2 |
∵以B为圆心,BC为半径作⊙B,
∴⊙B的半径为3,点C在圆上.
∵BC⊥AC,
∴直线AC与⊙B相切,C为切点,
∴A,E在圆外.
∵BD<3,
∴点D在圆内.
点评:本题考查的是点与圆的位置关系,熟知点与圆的3种位置关系是解答此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,AB是⊙O的直径,弦CD⊥AB,∠ACD=30°,CD=6,则由
如图,AB是⊙O的直径,弦CD⊥AB,∠ACD=30°,CD=6,则由 |
| AD |
A、
| ||
| B、π | ||
| C、2π | ||
| D、4π |
 如图:已知l1∥l2∥l3,CH=2cm,AG=1.5cm,BG=2.5cm,EF=5cm,求DH、EK的长.
如图:已知l1∥l2∥l3,CH=2cm,AG=1.5cm,BG=2.5cm,EF=5cm,求DH、EK的长.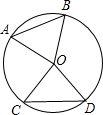 如图,在⊙O中,AB、CD是弦,根据条件填空.
如图,在⊙O中,AB、CD是弦,根据条件填空. 在平行四边形ABCD中,BE⊥AD,BF⊥CD,垂足为E、F,△BEF的垂心为H.若DG⊥BC,垂足为G,求证:BH=GF.
在平行四边形ABCD中,BE⊥AD,BF⊥CD,垂足为E、F,△BEF的垂心为H.若DG⊥BC,垂足为G,求证:BH=GF.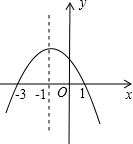 已知抛物线y=ax2+bx+c,如图所示,直线x=-1是其对称轴,
已知抛物线y=ax2+bx+c,如图所示,直线x=-1是其对称轴,