题目内容
过圆外一点P作⊙O的两条切线PA和PB,点A、点B为切点,∠P=40°,点D在AB上,点E和点F分别在PB和PA上,且AD=BE,BD=AF,求∠EDF的度数.
考点:切线的性质
专题:
分析:由条件可得∠PAB=∠PBA,结合条件可证明△ADF≌△BED,可得到∠AFD=∠EDB,再利用三角形内角和和平角的定义可得∠EDF=∠PAB,在△PAB中可求得∠PAB,则可得出∠EDF的度数.
解答: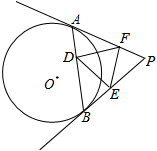 解:∵PA、PB都是⊙O的切线,
解:∵PA、PB都是⊙O的切线,
∴PA=PB,即有∠PAB=∠PBA,
在△ADF和△BED中,
,
∴△ADF≌△BED(SAS),
∴∠AFD=∠EDB,
∵∠FAD+∠FDA+∠AFD=180°,∠FDA+∠FDE+∠EDB=180°,
∴∠EDF=∠PAB,
∵∠PAB+∠PBA+∠P=180°,且∠PBA=∠PAB,
∴∠EDF=∠PAB=
=70°.
 解:∵PA、PB都是⊙O的切线,
解:∵PA、PB都是⊙O的切线,∴PA=PB,即有∠PAB=∠PBA,
在△ADF和△BED中,
|
∴△ADF≌△BED(SAS),
∴∠AFD=∠EDB,
∵∠FAD+∠FDA+∠AFD=180°,∠FDA+∠FDE+∠EDB=180°,
∴∠EDF=∠PAB,
∵∠PAB+∠PBA+∠P=180°,且∠PBA=∠PAB,
∴∠EDF=∠PAB=
| 180°-40° |
| 2 |
点评:本题主要考查切线长定理及全等三角形的判定和性质,在本题中找到∠EDF和∠PAB之间的关系是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案
相关题目
下列各数中,属于无理数的是( )
A、
| ||
B、
| ||
| C、(π-1)0 | ||
| D、2.121121112… |
 如图所示,几何体是由小正方体堆积而成的,其中每个正方体的棱长都是2cm.
如图所示,几何体是由小正方体堆积而成的,其中每个正方体的棱长都是2cm.
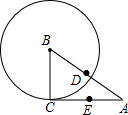 已知在Rt△ABC中,∠C=90°,BC=3cm,AC=4cm,D为AB的中点,E为AC的中点,以B为圆心,BC为半径作⊙B,A、C、D、E与⊙B的位置关系如何?
已知在Rt△ABC中,∠C=90°,BC=3cm,AC=4cm,D为AB的中点,E为AC的中点,以B为圆心,BC为半径作⊙B,A、C、D、E与⊙B的位置关系如何? 用网格中所给形状的纸片,只能折叠成一个无盖纸盒,为使纸盒有“盖“,需在图中再选画出一个小正方形.请你在图中把所有可能情况都指出来(在可选的小方格内依次填写一个数字)
用网格中所给形状的纸片,只能折叠成一个无盖纸盒,为使纸盒有“盖“,需在图中再选画出一个小正方形.请你在图中把所有可能情况都指出来(在可选的小方格内依次填写一个数字)