题目内容

如图，1=12，1+3=22，1+3+5=32，1+3+5+7=42，以此类推，1+3+5+7+9+…=
n2
n2
．
分析：观察1=12，1+3=22，1+3+5=32，1+3+5+7=42得到从1开始的几个连续奇数的和等于奇数的个数的平方，所以1+3+5+7+9+…+2n-1=n2．
解答：解：∵1=12，
1+3=22，
1+3+5=32，
1+3+5+7=42，
…
∴1+3+5+7+9+…+2n-1=n2．
故答案为：n2．
点评：本题考查了规律型：数字的变化类：认真观察、仔细思考，善用联想是解决这类问题的方法．
练习册系列答案
相关题目
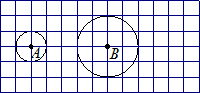11、如图，在12×6的网格图中（每个小正方形的边长均为1个单位），⊙A的半径为1，⊙B的半径为2，要使⊙A与静止的⊙B相切，那么⊙A由图示位置需向右平移
2、4、6或8
个单位．
精英家教网如图，用12米长的木方，做一个有一条横档的矩形窗子，为使透进的光线最多，选择窗子的长、宽各为
 
、
 
米．
16、如图，在12×12的正方形网格中，△TAB的顶点坐标分别为T（1，1）、A（2，3）、B（4，2）
（1）以点T（1，1）为位似中心，按比例尺（TA′：TA）=3：1在位似中心的同侧将△TAB放大为△TA′B′，放大后点A、B的对应点分别为A′、B′．画出△TA′B′，并写出点A′、B′的坐标；
（2）在（1）中，若C（a，b）为线段AB上任一点，写出变化后点C的对应点C′的坐标．
（2013•新余模拟）如图，共有12个大小相同的小正方形，其中阴影部分的5个小正方形是一个正方体的表面展开图的一部分，现从其余的小正方形中任取一个涂上阴影，能构成这个正方体的表面展开图的概率是
4
7
4
7
．
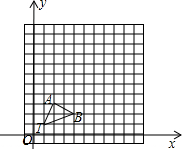如图，在12×12的正方形网格中，△TAB的顶点坐标分别为T（1，1）、A（2，3）、B（4，2）．以点T（1，1）为位似中心，按比例尺TA′：TA=3：1在位似中心的同侧将△TAB放大为△TA′B′，放大后点A、B的对应点分别为A′、B′，画出△TA′B′，写出点A′、B′坐标．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网