题目内容
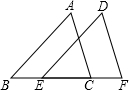 如图所示,在△ABC和△DEF中,B,E,C,F在同一条直线上.已知AC=DF,BE=CF,请你添加一个适当的条件
如图所示,在△ABC和△DEF中,B,E,C,F在同一条直线上.已知AC=DF,BE=CF,请你添加一个适当的条件考点:全等三角形的判定
专题:开放型
分析:由条件可得出BC=EF,且AC=DF,故可再加一组对应边相等或一组两边的夹角相等可证明全等.
解答:解:∵BE=CF,
∴BC=EF,且AC=DF,
所以当AB=DE时,
在△ABC和△DEF中,
,
∴△ABC≌△DEF(SSS),
或当∠ACB=∠DFE时,
在△ABC和△DEF中,
,
∴△ABC≌△DEF(SAS),
所以可添加AB=DE或∠ACB=∠DFE,
故答案为:AB=DE.
∴BC=EF,且AC=DF,
所以当AB=DE时,
在△ABC和△DEF中,
|
∴△ABC≌△DEF(SSS),
或当∠ACB=∠DFE时,
在△ABC和△DEF中,
|
∴△ABC≌△DEF(SAS),
所以可添加AB=DE或∠ACB=∠DFE,
故答案为:AB=DE.
点评:本题主要考查全等三角形的判定,掌握全等三角形的判定方法是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
下列说法中,错误的是( )
| A、实数与数轴上的点一一对应 |
| B、数轴上的点表示的数若不是有理数就是无理数 |
| C、有理数的运算及性质,在实数运算中仍成立 |
| D、对于实数a,若|a|=a,则a>0 |
天天基金网发布:中银活期宝货币2014年5月15日每万元收入1.2052元,16日比前一日增长0.0850元,17日比前一日减少0.1133元.若将17日比前一日的增长额记为-0.1133元,则16日比前一日的增长额应记为( )
| A、+0.1133元 |
| B、-0.0850元 |
| C、+0.0850元 |
| D、+1.2052元 |
下列各式中正确的是( )
A、-
| ||||
B、|-
| ||||
C、-
| ||||
D、-(-
|
设M=(a+b)2,N=(a-b)2+4ab,当a=-2,b=1
时,则M、N的值之间的关系是( )
| 1 |
| 4 |
| A、M>N | B、M=N |
| C、M<N | D、不确定 |