题目内容
19．已知直角三角形的两边长是方程9-（x-8）2=0的两根，求第三边的长．分析 先求出方程的解，再进行分类讨论即可．
解答 解：解方程9-（x-8）2=0得，x1=11，x2=5，
当11是直角三角形的斜边时，第三边=$\sqrt{{11}^{2}-{5}^{2}}$=4$\sqrt{6}$；
当11是直角三角形的直角边时，第三边=$\sqrt{{11}^{2}+{5}^{2}}$=$\sqrt{146}$．
综上所述，第三边的长为4$\sqrt{6}$或$\sqrt{146}$．
点评 本题考查的是勾股定理，熟知在任何一个直角三角形中，两条直角边长的平方之和一定等于斜边长的平方是解答此题的关键．
练习册系列答案
相关题目
9．若关于x、y的二元一次方程组$\left\{\begin{array}{l}{2x+y=a}\\{x-4y=2}\end{array}\right.$的解满足x-y＞1，则a的取值范围是（ ）
| A． | a＞-1 | B． | a＜2 | C． | a＞1 | D． | a＜4 |
8．在函数y=-$\frac{{a}^{2}+1}{x}$（a为常数）的图象上有点A（-1，y1），B（$\frac{1}{4}$，y2），C（$\frac{1}{2}$，y3），则函数值y1，y2，y3的大小关系是（ ）
| A． | y1＜y2＜y3 | B． | y3＜y2＜y1 | C． | y2＜y3＜y1 | D． | y2＜y1＜y3 |
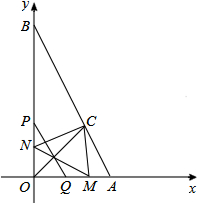如图，已知△OAB和△OQP在平面直角坐标系中，A（2，0），B（0，4），P为从O点出发，以每秒2个单位长的速度沿x轴向点B作匀速运动的动点，且PQ∥AB，PQ交x轴于点Q，∠AOB的平分线交AB于C，设P运动的时间为t（0＜t＜2）秒．