题目内容
如图，平行四边形 ABCD对角线交于点O，点E是线段BO上的动点（与点B、O不重合），连接CE，过A点作AF∥CE交BD于点F，连接AE与CF．
（1）求证：四边形AECF是平行四边形；
（2）当BA=BC=2，∠ABC=60°时，平行四边形 AECF能否成为正方形？若能，求出BE的长；若不能，请说明理由．
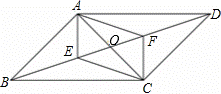
第23题
证明：证△AFD≌△BEC。。。。。。。。2分
∴AF=CE，∵AF∥CE，
∴四边形AECF是平行四边形．。。。。。3分（2）能．证得正方形得6分，求得BE得8分
练习册系列答案
阅读快车系列答案
相关题目
．1 B．12 C．
D．
；
实数k的值．
有意义，则a的取值范围是______________
．
B．
C．
D．